题目内容
某数学老师为了激发学生学习概率知识的兴趣，在课外活动时间开展了一次抽奖活动，其规则如下：①将抽奖箱中放入4个标号分别为1，2，3，4的质地、大小相同的小球．②由某个同学任意摸取得一个小球，记下小球上的数字，然后放回箱中，再摸取一个球仍记下小球上的数字．③只记小球上的数字，不记摸球的前后顺序．④若两次摸出小球的数字之积为“16”的是一等奖；数字之积为“3，6，9”的是二等奖；数字之积为其他情况的是三等奖．请你分别求出这个同学抽中一、二、三等奖的概率．
解：画出如图的树状图：
∴两次摸出小球的数字之积为“16”的次数为：1，总的结果有16个，
∴两次摸出小球的数字之积为“16”的概率为：
，
∴数字之积为“3，6，9”的次数为：5次，
∴两次摸出小球的数字之积为“3，6，9”的概率为：
；
∵数字之积为其他情况的是三等奖．
∴这个同学抽中三等奖的概率为：1--=
．
分析：列举出所有情况，让两次摸出的小球的标号之积为“16”或“3”“6”“9”的情况数除以总情况数即为所求的概率．
点评：此题考查的是用列表法或者用树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．树状图法适用于两步或两步以上完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．
∴两次摸出小球的数字之积为“16”的次数为：1，总的结果有16个，
∴两次摸出小球的数字之积为“16”的概率为：
，∴数字之积为“3，6，9”的次数为：5次，
∴两次摸出小球的数字之积为“3，6，9”的概率为：
；∵数字之积为其他情况的是三等奖．
∴这个同学抽中三等奖的概率为：1-
-=．分析：列举出所有情况，让两次摸出的小球的标号之积为“16”或“3”“6”“9”的情况数除以总情况数即为所求的概率．
点评：此题考查的是用列表法或者用树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．树状图法适用于两步或两步以上完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
某数学老师为了了解学生在数学学习中常见错误的纠正情况，收集了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对她所任教的初三（1）班和（2）班进行了检测．如图表示从两班各随机抽取的10名学生的得分情况：
（1）利用图中提供的信息，补全下表：
（2）若把24分以上（含24分）记为“优秀”，两班各有60名学生，请估计两班各有多少名学生成绩优秀；
（3）观察图中的数据分布情况，你认为哪个班的学生纠错的整体情况更好一些？
（1）利用图中提供的信息，补全下表：
| 班级 | 平均数（分） | 中位数（分） | 众数（分） |
| （1）班 | 24 | 24 | |
| （2）班 | 24 |
（3）观察图中的数据分布情况，你认为哪个班的学生纠错的整体情况更好一些？
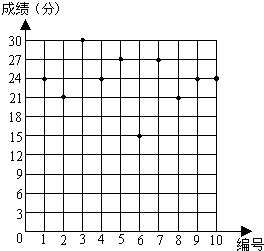的一个班进行了检测．已知这个班有50名学生，如图表示从这个班随机抽取的10名学生的得分情况：