题目内容
18. 如图,已知△ABC≌△DEF,∠B的对应角为∠E,∠A的对应角为∠D,若BE=7,CE=3,求CF的长.
如图,已知△ABC≌△DEF,∠B的对应角为∠E,∠A的对应角为∠D,若BE=7,CE=3,求CF的长.
分析 根据全等三角形的性质得BC=EF,则可得BF=CE=3,于是有BF+FC+CE=7,所以FC=1.
解答 解:∵△ABC≌△DEF,
∴BC=EF,
即BF+FC=CE+CF,
∴BF=CE=3,
∵BE=7,
∴BF+FC+CE=7,
即3+FC+3=7,
∴FC=1.
点评 本题考查了全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等;全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.下列式子成立的是( )
| A. | xy2-2y2•x=-xy2 | B. | 3a+5b=8ab | C. | 3ab-ab=2 | D. | a3•a2=a6 |
7.已知函数y=-$\frac{5}{4}$x2,点A(-1,y1)、B(-2,y2)、C(-3,y3)均在该函数的图象上,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y1<y3<y2 | D. | y2<y1<y3 |
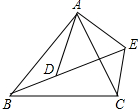 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$. 把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.
把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.