题目内容
 如图,在边长相同的小正方形组成的网格中,点A、B、C都在这些小正方形的顶点上,则tan∠BAC=
如图,在边长相同的小正方形组成的网格中,点A、B、C都在这些小正方形的顶点上,则tan∠BAC=| 1 |
| 2 |
| 1 |
| 2 |
分析:连接BC,再利用勾股定理分别计算出AB、AC、BC的长,然后再根据勾股定理逆定理证明∠BCA=90°,再利用三角函数定义可得答案.
解答: 解:连接BC,
解:连接BC,
AB=
=5,AC=
=
,CB=
=
,
∵(
)2+(
)2=52,
∴∠BCA=90°,
∴tan∠BAC=
=
=
,
故答案为:
.
 解:连接BC,
解:连接BC,AB=
| 32+42 |
| 42+22 |
| 20 |
| 12+22 |
| 5 |
∵(
| 5 |
| 20 |
∴∠BCA=90°,
∴tan∠BAC=
| CB |
| AC |
| ||
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:此题主要考查了勾股定理,勾股定理逆定理,以及锐角三角函数定义,关键是证明∠BCA=90°.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
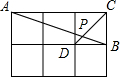 (2012•泰州)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是
(2012•泰州)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是 (2013•闸北区一模)如图,在边长相同的小正方形组成的网格中,点A、B、C都在这些小正方形的顶点上,则∠ABC的正切值是
(2013•闸北区一模)如图,在边长相同的小正方形组成的网格中,点A、B、C都在这些小正方形的顶点上,则∠ABC的正切值是 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则sin∠APD的值是
如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则sin∠APD的值是