题目内容
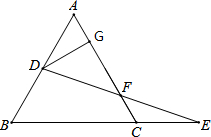 如图,D是等边△ABC的边AB上一点,E是BC延长线上一点,连接DE交AC于F,过D点作DG⊥AC于G点.
如图,D是等边△ABC的边AB上一点,E是BC延长线上一点,连接DE交AC于F,过D点作DG⊥AC于G点.(1)证明:AG=
| 1 | 2 |
(2)若DF=EF,求证:CE=AD.
分析:(1)由△ABC是等边三角形就可以得出∠A=60°,由DG⊥AC就可以得出∠AGD=90°,从而得出∠ADG=30°,就可以得出结论;
(2)过点D作DH∥BC交AC于点H,可以得到△DHF≌△ECF,就有DH=CE,再证明△ADH是等边三角形就可以得出结论.
(2)过点D作DH∥BC交AC于点H,可以得到△DHF≌△ECF,就有DH=CE,再证明△ADH是等边三角形就可以得出结论.
解答:解:(1)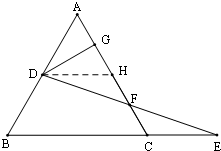 证明:∵△ABC是等边三角形,
证明:∵△ABC是等边三角形,
∴∠A=60°,
∵DG⊥AC,
∴∠AGD=90°,
∵∠ADG=30°,
∴AG=
AD;
(2)过点D作DH∥BC交AC于点H,
∴∠ADH=∠B,∠AHD=∠ACB,∠FDH=∠E,
∵△ABC是等边三角形,
∴∠B=∠ACB=∠A=60°,
∴∠A=∠ADH=∠AHD=60°,
∴△ADH是等边三角形,
∴DH=AD,
在△DHF和△ECF中,
,
∴△DHF≌△ECF(AAS),
∴DH=CE,
∴CE=AD.
 证明:∵△ABC是等边三角形,
证明:∵△ABC是等边三角形,∴∠A=60°,
∵DG⊥AC,
∴∠AGD=90°,
∵∠ADG=30°,
∴AG=
| 1 |
| 2 |
(2)过点D作DH∥BC交AC于点H,
∴∠ADH=∠B,∠AHD=∠ACB,∠FDH=∠E,
∵△ABC是等边三角形,
∴∠B=∠ACB=∠A=60°,
∴∠A=∠ADH=∠AHD=60°,
∴△ADH是等边三角形,
∴DH=AD,
在△DHF和△ECF中,
|
∴△DHF≌△ECF(AAS),
∴DH=CE,
∴CE=AD.
点评:本题考查了等边三角形判定及性质的运用,直角三角形的性质的运用,平行线的性质的运用,全等三角形的判定及性质的运用,解答时作DH∥BC是难点,证明三角形全等是关键.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE.
如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE. 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.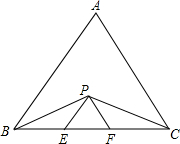 如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.
如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.