题目内容
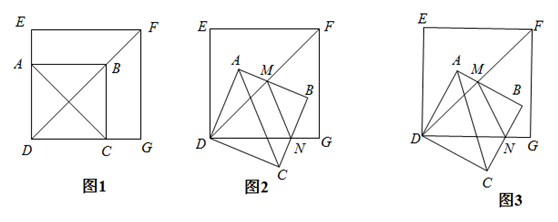
边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上(如图1),现将正方形ABCD绕D点顺时针旋转,当A点第一次落在DF上时停止旋转,旋转过程中, AB边交DF于点M,BC边交DG于点N.
(1)求边DA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时(如图2),求正方形ABCD旋转的度数;
(3)如图3,设△MBN的周长为p,在旋转正方形ABCD的过程中,p值是否有变化?请证明你的结论.
(1)求边DA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时(如图2),求正方形ABCD旋转的度数;
(3)如图3,设△MBN的周长为p,在旋转正方形ABCD的过程中,p值是否有变化?请证明你的结论.

(1) ;(2)
;(2) ;(3)不变化,证明见解析.
;(3)不变化,证明见解析.
 ;(2)
;(2) ;(3)不变化,证明见解析.
;(3)不变化,证明见解析.试题分析:(1)将正方形ABCD绕D点顺时针旋转,当A点第一次落在DF上时停止旋转,旋转过程中,DA旋转了
 ,从而根据扇形面积公式可求DA在旋转过程中所扫过的面积.
,从而根据扇形面积公式可求DA在旋转过程中所扫过的面积.(2)旋转过程中,当MN和AC平行时,根据平行的性质和全等三角形的判定和性质可求正方形ABCD旋转的度数为
 .
.(3)延长BA交DE轴于H点,通过证明
 和
和 可得结论.
可得结论.(1)∵A点第一次落在DF上时停止旋转,∴DA旋转了
 .
.∴DA在旋转过程中所扫过的面积为
 .
.(2)∵MN∥AC,∴
 ,
, .
.∴
 .∴
.∴ .
.又∵
 ,∴
,∴ .
.又∵
 ,∴
,∴ .
.∴
 .∴
.∴ .
.∴旋转过程中,当MN和AC平行时,正方形ABCD旋转的度数为
 .
.(3)不变化,证明如下:
如图, 延长BA交DE轴于H点,则
 ,
, ,
,∴
 .
.又∵
 .∴
.∴ .
.∴
 .
.又∵
 , ,∴
, ,∴ .
. ∴
 .∴
.∴ .
.∴
 .
.∴在旋转正方形ABCD的过程中,
 值无变化.
值无变化.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 ,CF⊥BD分别交BD、AD于点E、F,连接BF.
,CF⊥BD分别交BD、AD于点E、F,连接BF.




 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG= ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )

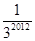





 ,﹣
,﹣ ,﹣
,﹣