题目内容
在矩形ABCD中,DC= ,CF⊥BD分别交BD、AD于点E、F,连接BF.
,CF⊥BD分别交BD、AD于点E、F,连接BF.
(1)求证:△DEC∽△FDC;
(2)当F为AD的中点时,求sin∠FBD的值及BC的长度.

 ,CF⊥BD分别交BD、AD于点E、F,连接BF.
,CF⊥BD分别交BD、AD于点E、F,连接BF.(1)求证:△DEC∽△FDC;
(2)当F为AD的中点时,求sin∠FBD的值及BC的长度.

(1)详见解析;(2)sin∠FBD= ;BC=
;BC= .
.
 ;BC=
;BC= .
.试题分析:(1)掌握三角形相似的判定方法,其中两角对应相等,两个三角形相似是最常用的方法.
(2)虽是求sin∠FBD,用的知识点都是三角形相似的性质,再用勾股定理,角的正弦公式可求出.
试题解析:证明:(1)∵∠DEC=∠FDC=90°,∠DCE=∠FCD,
∴△DEC∽△FDC.
(2)∵F为AD的中点,AD∥BC,
∴FE:EC=FD:BC=1:2,FB=FC,
∴FE:FC=1:3,
∴sin∠FBD=EF:BF=EF:FC=
 ;
;设EF=x,则FC=3x,
∵△DEC∽△FDC,
∴
 =
= ,即可得:6x2=6,
,即可得:6x2=6,解得:x=1,
则CF=3,
在Rt△CFD中,DF=
 ,
,∴BC=2DF=
 .
.
练习册系列答案
相关题目
 ,
, .
.
 时,
时, 上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
上,且⊙P是正方形ABCD的“等距圆”,则点P的坐标为_______________;
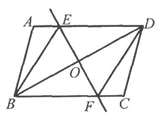
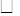 ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.