题目内容
 如图,直角边为2的两个全等的等腰直角三角形叠合在一起,将其中的一个沿AB移动,使重叠部分△A'PB的面积是1cm2,则移动的距离A′A=________ cm.
如图,直角边为2的两个全等的等腰直角三角形叠合在一起,将其中的一个沿AB移动,使重叠部分△A'PB的面积是1cm2,则移动的距离A′A=________ cm.
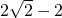
分析:由平移的性质,易得△A′PB是等腰直角三角形,然后过点C作CF⊥AB于F,过点P作PE⊥AB于E,易证得△BPE∽△BCF,又由△ABC是等腰直角三角形,△A'PB的面积是1cm2,即可求得AB与A′B的值,则可求得移动的距离A′A的长.
解答:
 解:过点C作CF⊥AB于F,过点P作PE⊥AB于E,
解:过点C作CF⊥AB于F,过点P作PE⊥AB于E,∴CF∥PE,
∴△BPE∽△BCF,
∴
 ,
,∵△ABC是等腰直角三角形,△A'PB的面积是1cm2,
∴CF=BC•sin∠ABC=BC•sin45°=2×
 =
= ,
, PB•PA′=1,
PB•PA′=1,∴PB=
 ,
,∴
 ,
,∴PE=1,
∵
 A′B•PE=1,AB=
A′B•PE=1,AB= =2
=2 ,
,∴A′B=2,
∴移动的距离A′A=2
 -2cm.
-2cm.故答案为:2
 -2.
-2.点评:此题考查了相似三角形的判定与性质,平移的性质,以及等腰直角三角形性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目

 如图,直角边为2的两个全等的等腰直角三角形叠合在一起,将其中的一个沿AB移动,使重叠部分△A'PB的面积是1cm2,则移动的距离A′A=
如图,直角边为2的两个全等的等腰直角三角形叠合在一起,将其中的一个沿AB移动,使重叠部分△A'PB的面积是1cm2,则移动的距离A′A=
