Question

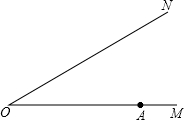如图，公路OM和公路ON在O处交汇，∠MON=30°，点A处有一所中学，OA=160米，设拖拉机行驶时，周围100米以内，会受噪音影响，那么拖拉机在公路ON由O向N方向行驶时，学校是否会受到噪音影响？设拖拉机速度为5米/秒，如果受影响，那么影响的时间是多长？

Answer 1

考点：勾股定理的应用

专题：

分析：过点A作AB⊥ON于B，则AB为A到道路的最短距离．在Rt△ABO中，可以求出AB=AO•sin30°，设AC、AD为正好受影响时，则AC=AD=100，在Rt△ABC中，BC²=AC²-AB²，由此可以求出BC，BD，又拖拉机速度为5m/s，让路程除以速度可以计算出受影响时间．

解答：解：学校会受到影响．
理由：过点A作AB⊥ON于B，
∵∠MON=30°，
∴AB=AOsin30°=80米＜100米，
∴学校会受到影响．
设拖拉机行至C处学校刚刚开始受影响，
超过D处时恰好不再受影响，
则AC=AD=100米，
在Rt△ABC中，由勾股定理得：BC=60米，
同理BD=60米∴CD=120米，
t=120÷5=24秒，
∴拖拉机速度为5米/秒，如果受影响，那么影响的时间是24秒．

点评：此题主要考查了勾股定理的应用，解此题的关键是把实际问题转化为数学问题，把实际问题抽象到解直角三角形中，进行解答；注意运用等腰三角形三线合一的性质得到受影响的路程．