题目内容
【题目】如图1,已知![]() ,
,![]() 分别为两坐标轴上的点,且
分别为两坐标轴上的点,且![]() ,
,![]() 满足
满足![]() ,且
,且![]() .
.
(1)求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
(2)若![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() ,设
,设![]() 、
、![]() 两点的横坐标分别为
两点的横坐标分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)如图2,若![]() ,点
,点![]() 是
是![]() 轴上
轴上![]() 点右侧一动点,
点右侧一动点,![]() 于点
于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,当点
,当点![]() 在点
在点![]() 右侧运动时,
右侧运动时,![]() 的度数是否改变?若不变,请求其值;若改变,请说明理由.
的度数是否改变?若不变,请求其值;若改变,请说明理由.
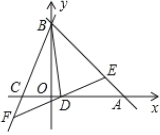
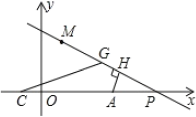
图1 图2
【答案】(1) A(12,0),B(0,12),C(4,0);
(2)![]()
(3) 不改变,![]()
【解析】
(1)由偶次方和绝对值的非负性质求出a和b的值,得出点A、B的坐标,再求出OC,即可得出点C的坐标;
(2)作EG⊥x轴于G,FH⊥x轴于H,DF=DE,由AAS证明△FDH≌△EDG,得出DH=DG,即可得出结果;
(3)连接MA、MC,过C作CT⊥PM于T,证明△CMT≌△MAH,可证明△CGT是等腰直角三角形,可求得∠CGM=45°.
(1)∵![]() ,
,
![]()
∴a12=0,b12=0,
∴a=b=12,
∴A(12,0),B(0,12),
∴OA=OB=12,
∵![]() .
.
∴OC=4,
∴C(4,0);
(2)作EG⊥x轴于G,FH⊥x轴于H,如图1所示:
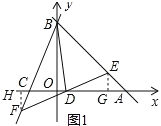
则![]()
在△FDH和△EDG中,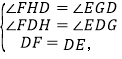
∴△FDH≌△EDG(AAS),
∴DH=DG,即![]()
∴![]()
(3)∠CGM的度数不改变,![]()
如图3,连接MA、MC,过C作CT⊥PM于T,过M作MS⊥x轴于点S,
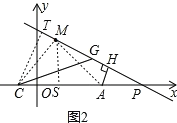
∵M(4,8),C(4,0),A(12,0),
∴S(4,0),
∴MS垂直平分AC,
∴MC=MA,且MS=SC,
∴![]()
∴![]()
∴∠TCM=∠AMH,
在△CMT和△MAH中
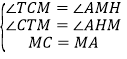
∴△CMT≌△MAH(AAS),
∴TM=AH,CT=MH,
又AH=HG
∴MT=GH,
∴GT=GM+MT=MG+GH=MH=CT,
∴△CGT是等腰直角三角形,
∴![]()
即当点P在点A右侧运动时,∠CGM的度数不改变.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案