题目内容
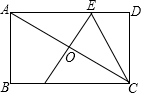（2013•揭西县模拟）如图，在矩形ABCD中，AB=3，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为| 25 |
| 8 |
| 25 |
| 8 |
分析：求出AE=CE，在Rt△DEC中，由勾股定理得出DE2+DC2=CE2，得出方程（4-CE）2+32=CE2，求出即可．
解答：解：∵四边形ABCD是矩形，
∴∠D=∠B=90°，AD=BC=4，AB=DC=3，
∵OE是AC的垂直平分线，
∴AE=CE，
∴DE=AD-AE=AD-CE=4-CE，
在Rt△DEC中，由勾股定理得：DE2+DC2=CE2，
（4-CE）2+32=CE2，
CE=
，
故答案为：
．
∴∠D=∠B=90°，AD=BC=4，AB=DC=3，
∵OE是AC的垂直平分线，
∴AE=CE，
∴DE=AD-AE=AD-CE=4-CE，
在Rt△DEC中，由勾股定理得：DE2+DC2=CE2，
（4-CE）2+32=CE2，
CE=
| 25 |
| 8 |
故答案为：
| 25 |
| 8 |
点评：本题考查了矩形性质，勾股定理，线段垂直平分线性质的应用，关键是能得出关于CE的方程．
练习册系列答案
相关题目
（2013•揭西县模拟）如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=10，CD=8，那么，sin∠OCE=（ ）
（2013•揭西县模拟）如图，两块相同的直角三角形完全重合在一起，∠A=30°，AC=10，把上面一块绕直角顶点B逆时针旋转到△A′B′C′的位置，点C′在AC上，A′C′与AB相交于点D，则C′D=（ ）