题目内容
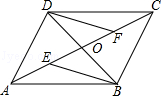
如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DF∥BE．
（1）求证：△BOE≌△DOF；
（2）若OD=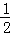
AC，则四边形ABCD是什么特殊四边形？请证明你的结论．
（1）证明：∵DF∥BE，
∴∠FDO=∠EBO，∠DFO=∠BEO，
∵O为AC的中点，即OA=OC，AE=CF，
∴OA﹣AE=OC﹣CF，即OE=OF，
在△BOE和△DOF中，
，
∴△BOE≌△DOF（AAS）；
（2）若OD=
AC，则四边形ABCD是矩形，理由为：
证明：∵△BOE≌△DOF，
∴OB=OD，
∴OA=OB=OC=OD，即BD=AC，
∴四边形ABCD为矩形
练习册系列答案
相关题目
已知二次函数y=ax2+bx+c的x、y的部分对应值如下表：
| x | ﹣1 | 0 | 1 | 2 | 3 |
| y | 5 | 1 | ﹣1 | ﹣1 | 1 |
则该二次函数图象的对称轴为（ ）
|
| A． | y轴 | B． | 直线x= | C． | 直线x=2 | D． | 直线x= |
如图是某个几何体的三视图，则该几何体的形状是（ ）
|
| A． | 长方体 | B． | 圆锥 | C． | 圆柱 | D． | 三棱柱 |
如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（ ）
|
| A． | （2，10） | B． | （﹣2，0） | C． | （2，10）或（﹣2，0） | D． | （10，2）或（﹣2，0） |
介于（ ）