题目内容
抛物线y=﹣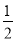 x2﹣x的顶点坐标是( )
x2﹣x的顶点坐标是( )
A. (1,﹣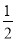 ) B. (﹣1,
) B. (﹣1, 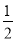 ) C. (
) C. (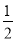 ,﹣1) D. (1,0)
,﹣1) D. (1,0)
4张扑克牌如图(1)所示放在桌子上,小敏把其中两张旋转180°后得到如图(2)所示,那么她所旋转的牌从左起是( )

A.第一张、第二张
B.第二张、第三张
C.第三张、第四张
D.第四张、第一张
查看答案已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
| … |
| 0 | 1 | 3 | … |
| … |
| 1 | 3 | 1 | … |
则下列判断中正确的是( )
A. 抛物线开口向上 B. 抛物线与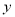 轴交于负半轴
轴交于负半轴
C. 当x=4时,y>0 D. 方程ax2+bx+c=0的正根在3与4之间
查看答案对于抛物线y=-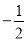 (x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数是( )
(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(-1,3);④x>1时,y随x的增大而减小,其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案下列命题中的真命题是( )
A. 全等的两个图形是中心对称图形
B. 关于中心对称的两个图形全等
C. 中心对称图形都是轴对称图形
D. 轴对称图形都是中心对称图形
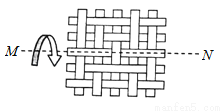
查看答案一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A.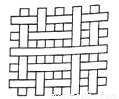 B.
B.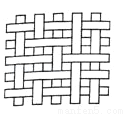 C.
C.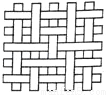 D.
D.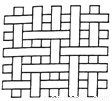
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
用a、b、c作三角形的三边,其中不能构成直角三角形的是( )
A. a2=(b+c)(b﹣c) B. a:b:c=1: 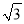 :2
:2
C. a=32,b=42,c=52 D. a=5,b=12,c=13
C 【解析】试题解析:∵a2=(b+c)(b﹣c), ∴a2=b2﹣c2 , ∴a2+c2=b2 , 根据勾股定理的逆定理可得,用a、b、c作三角形的三边,能构成直角三角形,故选项A错误; ∵a:b:c=1: :2, ∴设a=x,b=x,c=2x, ∵, ∴用a、b、c作三角形的三边,能构成直角三角形,故选项B错误; ∵a=32, b=42, ...如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是( )
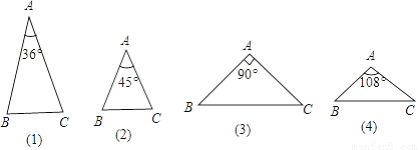
A. (1)(2)(3) B. (1)(3)(4) C. (2)(3)(4) D. (1)(2)(4)
查看答案如图,PB⊥AB于B,PC⊥AC于C,且PB=PC,则△APB≌△APC的理由是( )
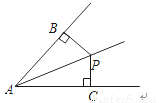
A. SAS B. ASA C. HL D. AAS
查看答案如图,在△ABC中,AB=AC=5,P是BC边上除B,C点外的任意一点,则代数式AP2+PB·PC等于 ( )
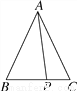
A. 25 B. 15 C. 20 D. 30
查看答案如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
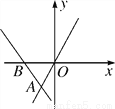
A. x<-2 B. -2<x<-1 C. -2<x<0 D. -1<x<0
查看答案若直线y=3x+6与直线y=2x+4的交点坐标为(a , b),则解为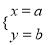 的方程组是( )
的方程组是( )
A. 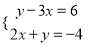 B.
B. 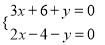 C.
C. 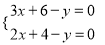 D.
D. 
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在数轴上离开原点4个长度单位的点表示的数是 ________ 。
4或-4 【解析】试题解析:到原点距离相等的点有两个,左边一个右边一个,所以答案为4或是-4.已知代数式2a3bn+1与﹣3am﹣2b2是同类项,则2m+3n=________.
查看答案一列单项式:﹣x2 , 3x3 , ﹣5x4 , 7x5 , …,按此规律排列,则第7个单项式为________
查看答案若|m﹣3|+(n+2)2=0,则m+2n的值为 .
查看答案如图,AC⊥BC于点C,CD⊥AB于点D,其中长度能表示点到直线(或线段)的距离的线段有( )
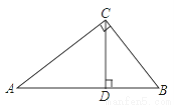
A. 1条 B. 2条 C. 3条 D. 5条
查看答案在数轴上,点A表示的数是﹣5,点C表示的数是4,若AB=2BC,则点B在数轴上表示的数是( )
A. 1或13 B. 1 C. 9 D. ﹣2或10
查看答案 试题属性- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
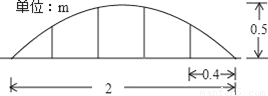
某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图)做成立柱,为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
(1)求此抛物线的解析式;
(2)计算所需不锈钢管的总长度.
某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?
查看答案如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1,D三点的坐标分别是(0,4),(0,3),(0,2).
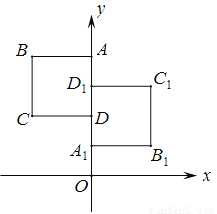
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
查看答案实践与操作:一般地,如果把一个图形绕着一个定点旋转一定角度α(α小于360°)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对称中心,α叫做这个旋转对称图形的一个旋转角,请根据上述规定解答下列问题:
(1)请写出一个有一个旋转角是90°旋转对称图形,这个图形可以是_____;
(2)尺规作图:在图中的等边三角形内部作出一个图形,使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形(作出的图形用实线,作图过程用虚线,保留痕迹,不写做法).
解一元二次方程
(1)x2﹣2x﹣1=0
(2)(2x﹣3)2=(x+2)2.
查看答案已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为_____.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
右图是“靠右侧通道行驶”的交通标志,若将图案绕其中心顺时针旋转90°,则得到的图案是“ ”的交通标志(不画图案,只填含义).

三角形两边长分别为3和6,第三边是方程x2﹣13x+36=0的根,则三角形的周长为 .
查看答案二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣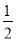 ,y2)、点C(
,y2)、点C(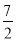 ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
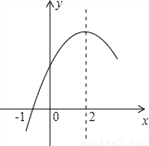
A. 2个 B. 3个 C. 4个 D. 5个
查看答案如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )
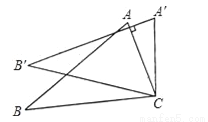
A. 50° B. 60° C. 70° D. 80°
查看答案关于x的一元二次方程x2﹣6x+2k=0有两个不相等的实数根,则实数k的取值范围是( )
A. k≤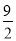 B. k<
B. k<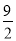 C. k≥
C. k≥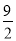 D. k>
D. k>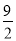
抛物线y=﹣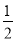 x2﹣x的顶点坐标是( )
x2﹣x的顶点坐标是( )
A. (1,﹣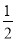 ) B. (﹣1,
) B. (﹣1, 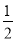 ) C. (
) C. (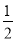 ,﹣1) D. (1,0)
,﹣1) D. (1,0)
- 题型:填空题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )

A. B.
B. C.
C. D.
D.
已知函数:①y=ax2;②y=3(x﹣1)2+2;③y=(x+3)2﹣2x2;④y=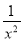 +x.其中,二次函数的个数为( )
+x.其中,二次函数的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案杭州市从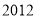 年
年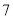 月
月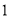 日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
日开始实行阶梯电价制,居民上生活用电价格方案如下:(本题不考虑峰谷电)
档次 | 全年的用电量 | 电价(单位:元/度) |
第一档 |
|
|
第二档 |
|
|
第三档 |
|
|
(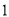 )小王家
)小王家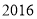 年全年的用电量是
年全年的用电量是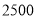 度,请计算小王家这年的电费付了多少元?
度,请计算小王家这年的电费付了多少元?
( )小李家
)小李家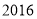 年
年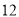 月份这个月的用电量是
月份这个月的用电量是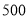 度,小李算出它们家的电费是
度,小李算出它们家的电费是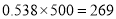 元,而供电局却收了小李家的电费
元,而供电局却收了小李家的电费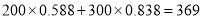 元,你知道其中的奥秘吗?请你来解释下.
元,你知道其中的奥秘吗?请你来解释下.
(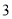 )小张家
)小张家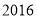 年全年用电量为
年全年用电量为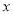 度,请用含
度,请用含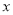 的代数式表示小张家全年应交的总电费,并把结果化简.
的代数式表示小张家全年应交的总电费,并把结果化简.
化简与求值:
(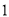 )已知当
)已知当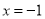 时,代数式
时,代数式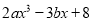 值为
值为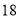 ,求代数式
,求代数式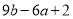 的值.
的值.
(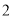 )已知
)已知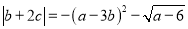 ,代数式
,代数式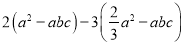 的值.
的值.
(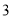 )若多项式
)若多项式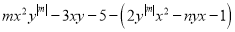 是关于
是关于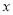 ,
, 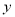 的四次二项式,求代数式
的四次二项式,求代数式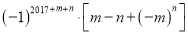 的值.
的值.
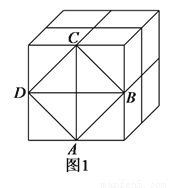
如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形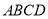 ,求出阴影部分的面积及其边长.
,求出阴影部分的面积及其边长.
(3)把正方形 放到数轴上,如图
放到数轴上,如图 ,使得
,使得 与
与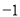 重合,点
重合,点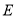 与
与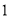 重合,点
重合,点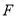 与点
与点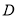 关于
关于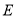 点对称,那么
点对称,那么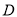 在数轴上表示的数为__________;点
在数轴上表示的数为__________;点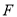 在数轴上表示的数为__________.
在数轴上表示的数为__________.
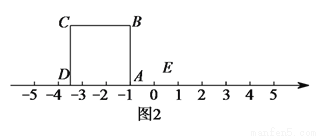
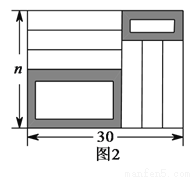
把六张形状大小完全相同的小长方形卡片(其中较短的一边长为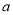 厘米,如图
厘米,如图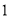 )不重叠地放在一个底面为长方形(长为
)不重叠地放在一个底面为长方形(长为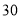 厘米,宽为
厘米,宽为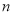 厘米)的盒子底部(如图
厘米)的盒子底部(如图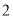 ),盒子底面未被卡片覆盖的部分分别用
),盒子底面未被卡片覆盖的部分分别用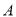 ,
,  表示,请观察图形,回答问题:
表示,请观察图形,回答问题:
(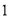 )求矩形
)求矩形 的长和宽(用含
的长和宽(用含 或
或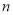 的代数式表示).
的代数式表示).
( )当图中两块长方形阴影部分
)当图中两块长方形阴影部分 ,
, 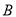 的周长和(用含
的周长和(用含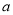 或
或 的代数式表示).
的代数式表示).
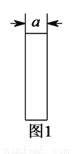
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
在数轴上表示下列个数,并用“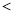 ”连接起来.(要求以
”连接起来.(要求以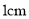 为单位长度画数轴)
为单位长度画数轴)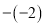 ,
,  ,
, 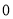 ,
, 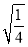 ,
, 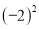 ,
,  .
.
计算:(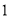 )
)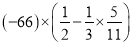 .
.
(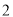 )
)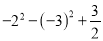 .
.
(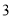 )
) .
.
(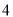 )
)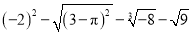 .
.
已知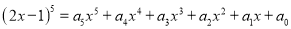 是关于
是关于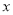 的恒等式,则
的恒等式,则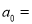 __________.且
__________.且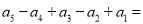 __________.
__________.
若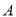 与
与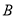 都是三次多项式,
都是三次多项式, 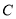 是五次多项式,有下列说法:①
是五次多项式,有下列说法:①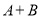 可能是六次多项式;②
可能是六次多项式;②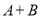 一定是次数不高于三次的整式;③
一定是次数不高于三次的整式;③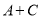 一定五次多项式;④
一定五次多项式;④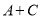 一定是五次整式;⑤
一定是五次整式;⑤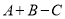 可能是常数.其中正确的是__________.
可能是常数.其中正确的是__________.
已知有理数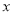 ,
, 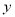 满足:
满足: 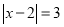 ,
, 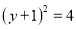 且
且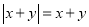 ,则
,则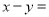 __________.
__________.
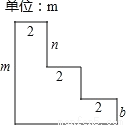
如图是一个摆放礼物的柜子截面的示意图,每一个转角都是直角,数据如图所示.则该图形的周长为__________.面积为__________.(用含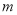 ,
, 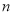 ,
, 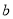 的代数式表示化简后的结果)
的代数式表示化简后的结果)
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列计算正确的是( ).
A. 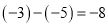 B.
B. 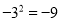 C.
C. 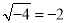 D.
D. 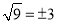
如图,已知∠MON=90º,A是∠MON内部的一点,过点A作AB⊥ON,垂点为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动。设运动时间为t秒(t>0)。
(1)当t=1秒时,ΔEOF与ΔABO是否相似?请说明理由。
(2)在运动过程中,不论t取何值时,总有EF⊥OA,为什么?
(3)连接AF,在运动过程中,是否存在某一时刻t,使得SΔAEF=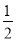 S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
S四边形ABOF ?若存在,请求出此时t的值;若不存在,请说明理由。
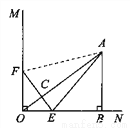
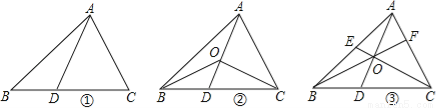
如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是BC边上的中点时,S△ABD:S△ABC= ;当点D是BC边上任意一点时,S△ABD:S△ABC= (用图中已有线段表示).
探索研究:
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、D重合),连结BO并延长交AC于点F,连结CO并延长交AB于点E,试猜想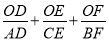 的值,并说明理由.
的值,并说明理由.
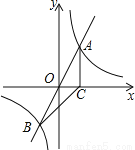
如图, 正比例函数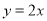 的图象与反比例函数
的图象与反比例函数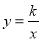 的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连接BC,若ΔABC面积为 2.
(1)求k的值
(2)x轴上是否存在一点D,使ΔABD是以AB为斜边的直角三角形?若存在,求出点D的坐标,若不存在,说明理由。
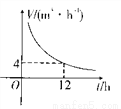
如图是某一蓄水池每1h的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数图象。
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)写出函数的函数表达式;
(3)若要6h排完水池的水,那么每1h的排水量应该是多少?
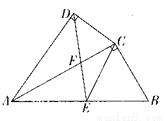
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90º,E为AB的中点,求证:
(1)AC2=AB·AD;
(2)CE∥AD。
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图,菱形ABCD的周长为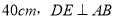 ,垂足为
,垂足为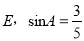 ,则下列结论正确的有
,则下列结论正确的有
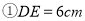 ;
; 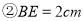 ;
;  菱形面积为
菱形面积为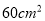 ;
; 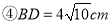 .
.
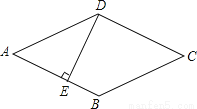
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】试题解析:∵菱形ABCD的周长为40cm, ∴AD=AB=BC=CD=10. ∵DE⊥AB,垂足为E, ∴菱形的面积为: 在中, ∴①②③正确,④错误; ∴结论正确的有三个. 故选C.为执行“均衡教育”政策,某县2014年投入教育经费2500万元,预计到2016年底三年累计投入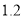 亿元
亿元 若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是
若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是
A. 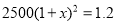
B. 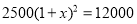
C. 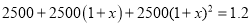
D. 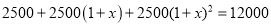
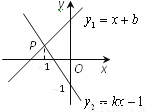
如图所示,直线y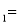 x
x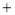 b与y
b与y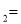 kx
kx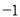 相交于点P,点P的横坐标为
相交于点P,点P的横坐标为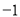 ,则关于x的不 等式x
,则关于x的不 等式x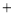 b
b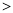 kx
kx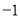 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是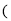
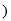
A. 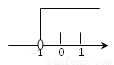
B. 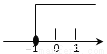
C. 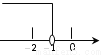
D. 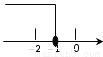
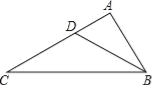
如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果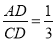 ,那么
,那么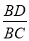 =( )
=( )
A. B.
B. C.
C. D.
D. 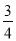
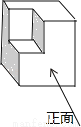
如图所示的几何体的俯视图是
A.  B.
B.  C.
C.  D.
D. 
下列运算正确的是
A. 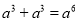 B.
B. 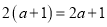 C.
C. 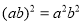 D.
D. 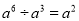
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
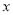
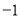
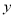
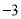

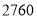 度以内(包括
度以内(包括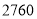 度)
度)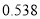
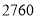 至
至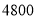 度(包含
度(包含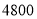 度)
度)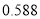
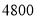 度以上
度以上