题目内容
 如图,△ABC中,∠C=90°,BC=6,AC=8,PQ∥AB,点P在AC上(与点A、C不重合),点Q在BC上.试问:在AB上是否存在点M,使△PQM为等腰直角三角形?若存在,求PQ的长;若不存在,请说明理由.
如图,△ABC中,∠C=90°,BC=6,AC=8,PQ∥AB,点P在AC上(与点A、C不重合),点Q在BC上.试问:在AB上是否存在点M,使△PQM为等腰直角三角形?若存在,求PQ的长;若不存在,请说明理由.
解:AC=8,BC=6,由勾股定理得:AB=10,
设PC=x,
∵PQ∥AB,
∴ =
= ,
,
∵PC=x,BC=10,AC=8,代入可求出 ,
,
∵△PQM为等腰直角三角形,
∴讨论哪个角为直角如下:
(1)当∠MPQ为直角时,则可得 ,
,
∴ ,
,
在△ABC中 ,而在△PMA中
,而在△PMA中 ,
,
∴得 ,从而
,从而 .(若∠MQP为直角类似)
.(若∠MQP为直角类似)
(2)当∠PMQ为直角时,则可得PM=MQ=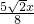 ,
,
过P作PN⊥AB于N,
易得 ,
,
同(1)得
∴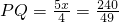 .
.
分析:由于PQ的位置是变化的,故可以使△PQM为等腰直角三角形,设PC=x,当△PQM为等腰直角三角形时,有三种情况:
1、当∠MPQ为直角时,可得到PM=PQ= x,而在△ABC中
x,而在△ABC中 ,而在△PMA中
,而在△PMA中 ,建立方程可求得x的值,从而求得PQ的值.
,建立方程可求得x的值,从而求得PQ的值.
2、若∠MQP为直角,与1类似;
3、当∠PMQ为直角时,则可得PQ=MQ=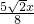 ,过P作PN⊥AB于N,易得
,过P作PN⊥AB于N,易得 ,即可求得PQ的值.
,即可求得PQ的值.
点评:本题利用了等腰直角三角形的性质,正弦的概念求解.
设PC=x,
∵PQ∥AB,
∴
 =
= ,
,∵PC=x,BC=10,AC=8,代入可求出
 ,
,∵△PQM为等腰直角三角形,
∴讨论哪个角为直角如下:
(1)当∠MPQ为直角时,则可得
 ,
,∴
 ,
,在△ABC中
 ,而在△PMA中
,而在△PMA中 ,
,∴得
 ,从而
,从而 .(若∠MQP为直角类似)
.(若∠MQP为直角类似)(2)当∠PMQ为直角时,则可得PM=MQ=
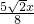 ,
,过P作PN⊥AB于N,
易得
 ,
,同(1)得

∴
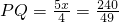 .
.分析:由于PQ的位置是变化的,故可以使△PQM为等腰直角三角形,设PC=x,当△PQM为等腰直角三角形时,有三种情况:
1、当∠MPQ为直角时,可得到PM=PQ=
 x,而在△ABC中
x,而在△ABC中 ,而在△PMA中
,而在△PMA中 ,建立方程可求得x的值,从而求得PQ的值.
,建立方程可求得x的值,从而求得PQ的值.2、若∠MQP为直角,与1类似;
3、当∠PMQ为直角时,则可得PQ=MQ=
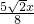 ,过P作PN⊥AB于N,易得
,过P作PN⊥AB于N,易得 ,即可求得PQ的值.
,即可求得PQ的值.点评:本题利用了等腰直角三角形的性质,正弦的概念求解.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.