题目内容
【题目】计算：
（1）解方程：①（2x﹣3）2＝25
②
﹣
＝x
（2）先化简，再求值：（1﹣
）÷
﹣
，其中x满足x2﹣x﹣l＝0
【答案】（1）①x1＝4．x2＝﹣1；②x＝﹣1；（2）
，1
【解析】
（1）①利用直接开平方法求解；②去分母，化分式方程为整式方程，利用十字相乘法求解，继而进行检验即可得；
（2）括号内先通分进行分式的加减运算，然后再进行分式的除法运算，最后按顺序进行计算化简分式，再变形x2﹣x﹣l＝0代入求值．
解：（1）①由原式可得：2x﹣3＝±5，即2x＝±5+3，
∴x＝
所以x1＝4．x2＝﹣1
②方程的两边都乘以（x﹣4），得3﹣x+1＝x2﹣4x
整理，得x2﹣3x﹣4＝0
因式分解得：（x﹣4）（x+1）＝0
∴x1＝4．x2＝﹣1
经检验，x＝4不是原方程的根
所以原分式方程的解为：x＝﹣1．
（2）（1﹣
）÷
﹣
＝
＝x﹣
＝
∵x2﹣x﹣l＝0，
即x2＝x+l
所以原式＝1.
练习册系列答案
相关题目
【题目】二次函数
上部分点的横坐标x与纵坐标y的对应值如下表：
x | … |
|
| 0 | 1 | 2 | 3 | … |
y | … | 3 |
| 0 |
| 0 | m | … |
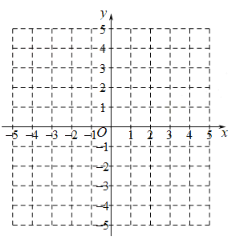
（1）直接写出此二次函数的对称轴 ；
（2）求b的值；
（3）直接写出表中的m值，m= ；
（4）在平面直角坐标系xOy中，画出此二次函数的图象．
