题目内容
如图,二次函数y=ax2+bx+2的图象与x轴、y轴的交点分别为A、B,点C在这个二次函数的 图象上,且∠ABC=90°,∠CAB=∠BAO,
图象上,且∠ABC=90°,∠CAB=∠BAO, .
.
(1)求点A的坐标;
(2)求这个二次函数的解析式.
解:(1)二次函数y=ax2+bx+2的图象y轴的交点为B(0,2),
在Rt△AOB中,
∵OB=2, ,
,
∴OA=4,
∴点A的坐标(4,0).
(2)过点C作CD⊥y轴,垂足为D,
∵∠CDB=∠ABC=∠AOB=90°,
∴∠CBD=180°-∠ABC-∠ABO=90°-∠ABO=∠BAO.
∴△CDB∽△BOA,
∵∠CAB=∠BAO,
∴ ,
,
∴ .
.
∵OB=2,
∴CD=1,BD=2,
∴OD=4.
∴C(1,4).
∵点A、C在二次函数y=ax2+bx+2的图象上,
∴
∴
∴二次函数解析式为 .
.
分析:(1)首先根据二次函数y=ax2+bx+2的y轴的交点B,确定出B点的坐标值(即可知线段OB的长).再利用三角函数 ,求得线段OA的长,进而确定出A点的坐标值.
,求得线段OA的长,进而确定出A点的坐标值.
(2)由(1)知A点的坐标值,再求得C点的坐标值,联立组成方程组即可解得a、b的值.要求C点的值,因而过点C作CD⊥y轴,垂足为D.首先证得Rt△CDB∽Rt△BOA,利用相似三角形的性质求得CD、DB的长,进而得到C点的坐标值.
点评:本题是一道二次函数的综合题,主要考查了二次函数解析式的确定、函数图象交点的求法、相似三角形的判定与性质、三角函数等知识点.另外巧妙添加辅助线CD构造直角三角形,也是解题成功的一个关键因素;该题也是数形结合数学思想的典型题例.
在Rt△AOB中,
∵OB=2,
 ,
,∴OA=4,
∴点A的坐标(4,0).
(2)过点C作CD⊥y轴,垂足为D,
∵∠CDB=∠ABC=∠AOB=90°,
∴∠CBD=180°-∠ABC-∠ABO=90°-∠ABO=∠BAO.
∴△CDB∽△BOA,

∵∠CAB=∠BAO,
∴
 ,
,∴
 .
.∵OB=2,
∴CD=1,BD=2,
∴OD=4.
∴C(1,4).
∵点A、C在二次函数y=ax2+bx+2的图象上,
∴

∴

∴二次函数解析式为
 .
.分析:(1)首先根据二次函数y=ax2+bx+2的y轴的交点B,确定出B点的坐标值(即可知线段OB的长).再利用三角函数
 ,求得线段OA的长,进而确定出A点的坐标值.
,求得线段OA的长,进而确定出A点的坐标值.(2)由(1)知A点的坐标值,再求得C点的坐标值,联立组成方程组即可解得a、b的值.要求C点的值,因而过点C作CD⊥y轴,垂足为D.首先证得Rt△CDB∽Rt△BOA,利用相似三角形的性质求得CD、DB的长,进而得到C点的坐标值.
点评:本题是一道二次函数的综合题,主要考查了二次函数解析式的确定、函数图象交点的求法、相似三角形的判定与性质、三角函数等知识点.另外巧妙添加辅助线CD构造直角三角形,也是解题成功的一个关键因素;该题也是数形结合数学思想的典型题例.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
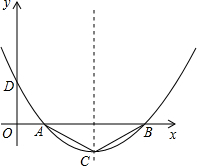 如图,二次函数的图象经过点D(0,
如图,二次函数的图象经过点D(0,
 如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式.
如图,二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于点A(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数解析式. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题: 如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b
如图,二次函数y=ax2+bx+c的图象与x轴相交于两个点,根据图象回答:(1)b