题目内容
已知A(1,5)和B(m,-2)是一次函数y=kx+b的图象与反比例函数y=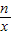 的图象的两个交点.
的图象的两个交点.(1)求m的值和函数y=
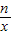 的解析式;
的解析式;(2)在同一直角坐标系中画出这两个函数的大致图象,并根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
【答案】分析:(1)先把点A(1,5)代入y=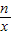 ,求出n的值,即可得到反比例函数y=
,求出n的值,即可得到反比例函数y=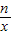 的解析式,再把y=-2代入,求出对应的x即m的值;
的解析式,再把y=-2代入,求出对应的x即m的值;
(2)把A(1,5)和B(m,-2)代入y=kx+b,运用待定系数法求出一次函数的解析式,根据一次函数及反比例函数的解析式,结合它们的图象性质可在同一直角坐标系中画出这两个函数的大致图象;观察图象,直线落在曲线上方的部分所对应的x的值即为所求.
解答: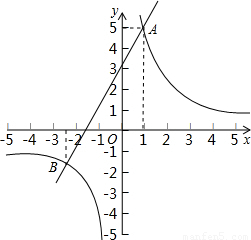 解:(1)把点A(1,5)代入y=
解:(1)把点A(1,5)代入y=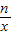 ,
,
得5=n,即n=5.
∴反比例函数的解析式为y= .
.
当y=-2时,有-2= ;
;
∴m=- .
.
(2)把A(1,5)和B(- ,-2)代入y=kx+b,
,-2)代入y=kx+b,
得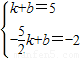 ,
,
解得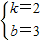 .
.
∴一次函数的解析式为y=2x+3.
在同一直角坐标系中画出函数y= 与y=2x+3的图象,如右图所示,
与y=2x+3的图象,如右图所示,
观察图象,可知当- <x<0或x>1时,一次函数的值大于反比例函数的值.
<x<0或x>1时,一次函数的值大于反比例函数的值.
点评:本题主要考查了运用待定系数法求函数的解析式,一次函数与反比例函数的图象性质.
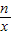 ,求出n的值,即可得到反比例函数y=
,求出n的值,即可得到反比例函数y=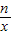 的解析式,再把y=-2代入,求出对应的x即m的值;
的解析式,再把y=-2代入,求出对应的x即m的值;(2)把A(1,5)和B(m,-2)代入y=kx+b,运用待定系数法求出一次函数的解析式,根据一次函数及反比例函数的解析式,结合它们的图象性质可在同一直角坐标系中画出这两个函数的大致图象;观察图象,直线落在曲线上方的部分所对应的x的值即为所求.
解答:
 解:(1)把点A(1,5)代入y=
解:(1)把点A(1,5)代入y=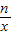 ,
,得5=n,即n=5.
∴反比例函数的解析式为y=
 .
.当y=-2时,有-2=
 ;
;∴m=-
 .
.(2)把A(1,5)和B(-
 ,-2)代入y=kx+b,
,-2)代入y=kx+b,得
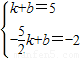 ,
,解得
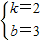 .
.∴一次函数的解析式为y=2x+3.
在同一直角坐标系中画出函数y=
 与y=2x+3的图象,如右图所示,
与y=2x+3的图象,如右图所示,观察图象,可知当-
 <x<0或x>1时,一次函数的值大于反比例函数的值.
<x<0或x>1时,一次函数的值大于反比例函数的值.点评:本题主要考查了运用待定系数法求函数的解析式,一次函数与反比例函数的图象性质.

练习册系列答案
相关题目
 已知:如图,扇形OAB和扇形OA′B′的圆心角相同,设AA′=BB′=d.
已知:如图,扇形OAB和扇形OA′B′的圆心角相同,设AA′=BB′=d.