题目内容
抛物线y=2x2与直线y=3x-b只有一个公共点，则b=分析：将直线y=3x-b代入解析式y=2x2得到2x2-3x+b=0，利用根的判别式即可求出b的值．
解答：解：将直线y=3x-b代入解析式y=2x2得到2x2-3x+b=0，
因为抛物线y=2x2与直线y=3x-b只有一个公共点，
所以△=9-4×2b=0，
解得，b=
．
因为抛物线y=2x2与直线y=3x-b只有一个公共点，
所以△=9-4×2b=0，
解得，b=
| 9 |
| 8 |
点评：此题考查了抛物线与直线交点坐标与其解析式组成的方程组的交点坐标的关系，要明确：方程组的解即为交点坐标．
练习册系列答案
相关题目
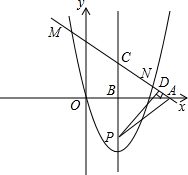、N两点．
的顶点为M，直线y2=x，点P（n，0）为x轴上的一个动点，过点P作x轴的垂线分别交抛物线y1=2x2+
和直线y2=x于点A，点B．
，求a，b，c的值．