题目内容
如图，△ABC中，∠BAC=120°，AB=AC，BC=4，请你建立适当的直角坐标系，并写出A，B，C各点的坐标．
解：答案不唯一，可以是：如图，
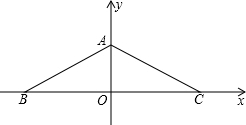
以BC所在的直线为x轴，BC的垂直平分线为y轴，垂直平分线与BC的交点为原点建立直角坐标系；
∵∠BAC=120°，AB=AC，
故y轴必经过A点，
∴∠BCA=∠ABC=30°，BO=OC=
BC=2，
∴在Rt△AOC中，OA=OC•tan∠ACB=2tan30°=
，
∴A（0，），B（-2，0），C（2，0）．
分析：本题的答案不唯一，但主要应用的是x、y轴互相垂直的条件来构建直角三角形运用三角函数进行求解．
点评：本题考查基本几何知识和平面直角坐标系，属于开放题．
以BC所在的直线为x轴，BC的垂直平分线为y轴，垂直平分线与BC的交点为原点建立直角坐标系；
∵∠BAC=120°，AB=AC，
故y轴必经过A点，
∴∠BCA=∠ABC=30°，BO=OC=
BC=2，∴在Rt△AOC中，OA=OC•tan∠ACB=2tan30°=
，∴A（0，
），B（-2，0），C（2，0）．分析：本题的答案不唯一，但主要应用的是x、y轴互相垂直的条件来构建直角三角形运用三角函数进行求解．
点评：本题考查基本几何知识和平面直角坐标系，属于开放题．
练习册系列答案
相关题目
26、已知：如图，△ABC中，点D在AC的延长线上，CE是∠DCB的角平分线，且CE∥AB．
27、已知：如图，△ABC中，∠BAC=60°，D、E两点在直线BC上，连接AD、AE．
27、如图，△ABC中，AD⊥BC于D，DN⊥AC于N，DM⊥AB于M
14、如图，△ABC中，∠BAC=120°，AD⊥BC于D，且AB+BD=DC，则∠C的大小是（ ）
已知，如图，△ABC中，点D在BC上，且∠1=∠C，∠2=2∠3，∠BAC=70°．