题目内容

如图，菱形AB₁C₁D₁的边长为1，∠B₁=30°，作AD₂⊥B₁C于点D₂，以AD₂为一边，做第二个菱形AB₂C₂D，使∠B₂=30°；作AD₃⊥B₂C于点D₃，以AD₃为一边做第三个菱形AB₃C₃D₃，使∠B₃=30°…依此类推，这样做的第n个菱形AB_nC_nD_n的边AD_n的长是________．

$\text{[math]}$
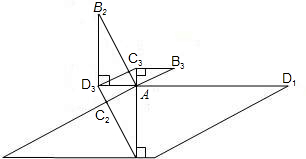
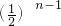
分析：根据菱形的四条边都相等可得各边都相等，又因为直角三角形中30°的锐角所对的直角边等于斜边的一半，所以易得AD₂的长，同理，可得AD₃的长，即可求得AD_n的长．
解答：∵菱形AB₁C₁D₁的边长为1，∠B₁=30°，
作AD₂⊥B₁C₁于点D₂，
∴AD₂= $\text{[math]}$ AB₁= $\text{[math]}$ ，
以AD₂为一边，做第二个菱形AB₂C₂D₂，使∠B₂=30°；
同理：作AD₃⊥B₂C₂于点D，
∴AD₃= $\text{[math]}$ AB₂= $\text{[math]}$ AD₂= $\text{[math]}$ × $\text{[math]}$ = $\text{[math]}$ ；
以AD₃为一边做第三个菱形AB₃C₃D₃，使∠B₃=30°；…依此类推，
这样做的第4个菱形的边长为：AD₄= $\text{[math]}$ ；
这样做的第n个菱形AB_nC_nD_n的边AD_n的长是 $\text{[math]}$ ，或者写成： $\text{[math]}$ ．
点评：此题考查了菱形的性质与直角三角形的性质（直角三角形中30°的锐角所对的直角边等于斜边的一半）．注意此题属于规律提，比较难，解题时需要认真分析．

练习册系列答案

节节高解析测评系列答案

海淀金卷系列答案

全能金卷全能卷王系列答案

名师优选全程练考卷系列答案

本真试卷系列答案

能考试期末冲刺卷系列答案

课时必胜系列答案

小学生每日5分钟口算系列答案

伴你成长课时练系列答案

随堂练习与单元测试系列答案

相关题目

如图，菱形AB₁C₁D₁的边长为1，∠B₁=60°；作AD₂⊥B₁C₁于点D₂，以AD₂为一边，做第二个菱形AB₂C₂D₂，使∠B₂=60°；作AD₃⊥B₂C₂于点D₃，以AD₃为一边做第三个菱形AB₃C₃D₃，使∠B₃=60°…依此类推，这样做的第n个菱形AB_nC_nD_n的边AD_n的长是

如图，菱形AB₁C₁D₁的边长为1，∠B₁=30°，作AD₂⊥B₁C于点D₂，以AD₂为一边，做第二个菱形AB₂C₂D，使∠B₂=30°；作AD₃⊥B₂C于点D₃，以AD₃为一边做第三个菱形AB₃C₃D₃，使∠B₃=30°…依此类推，这样做的第n个菱形AB_nC_nD_n的边AD_n的长是

如图，菱形AB₁C₁D₁的边长为1，∠B₁=30°，作AD₂⊥B₁C于点D₂，以AD₂为一边，做第二个菱形AB₂C₂D，使∠B₂=30°；作AD₃⊥B₂C于点D₃，以AD₃为一边做第三个菱形AB₃C₃D₃，使∠B₃=30°…依此类推，这样做的第n个菱形AB_nC_nD_n的边AD_n的长是．

如图，菱形AB₁C₁D₁的边长为1，∠B₁=60°；作AD₂⊥B₁C₁于点D₂，以AD₂为一边，做第二个菱形AB₂C₂D₂，使∠B₂=60°；作AD₃⊥B₂C₂于点D₃，以AD₃为一边做第三个菱形AB₃C₃D₃，使∠B₃=60°…依此类推，这样做的第n个菱形AB_nC_nD_n的边AD_n的长是．

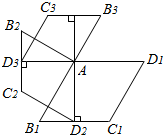如图，菱形AB₁C₁D₁的边长为1，∠B₁=60°；作AD₂⊥B₁C₁于点D₂，以AD₂为一边，做第二个菱形AB₂C₂D₂，使∠B₂=60°；作AD₃⊥B₂C₂于点D₃，以AD₃为一边做第三个菱形AB₃C₃D₃，使∠B₃=60°…依此类推，这样做的第n个菱形AB_nC_nD_n的边AD_n的长是．