题目内容
7.先化简,再求值:($\frac{a+b}{2a{b}^{2}}$)3÷($\frac{{a}^{2}-{b}^{2}}{a{b}^{3}}$)2$÷[\frac{1}{2(a-b)}]$2,其中a=$\frac{1}{2}$,b=$\frac{2}{3}$.
分析 原式先计算乘方运算,再计算乘除运算得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{(a+b)^{3}}{8{a}^{3}{b}^{6}}$•$\frac{{a}^{2}{b}^{6}}{(a+b)^{2}(a-b)^{2}}$•4(a-b)2=$\frac{a+b}{2a}$,
当a=$\frac{1}{2}$,b=$\frac{2}{3}$时,原式=$\frac{\frac{1}{2}+\frac{2}{3}}{2×\frac{1}{2}}$=$\frac{7}{6}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.下列式子正确的是( )
| A. | |π-3|=3-π | B. | 若ax=ay,则x=y | C. | a+b>a-b | D. | $-\frac{2}{-9}=\frac{2}{9}$ |
 如图,点P在函数y=-x的图象上运动,点A的坐标为(1,0),当线段AP最短时,点P的坐标为($\frac{1}{2},-\frac{1}{2}$).
如图,点P在函数y=-x的图象上运动,点A的坐标为(1,0),当线段AP最短时,点P的坐标为($\frac{1}{2},-\frac{1}{2}$).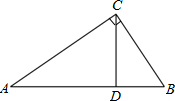 如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.
如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.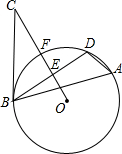 如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.