题目内容
【题目】在![]() 中,
中,![]() ,
,![]() .
.

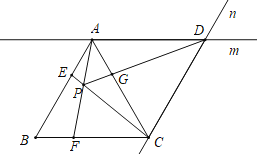
(Ⅰ)如图Ⅰ,![]() 为
为![]() 边上一点(不与点
边上一点(不与点![]() 重合),将线段
重合),将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
求证:(1)![]() ;
;
(2)![]() .
.
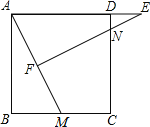
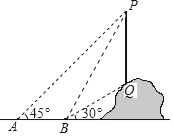
(Ⅱ)如图Ⅱ,![]() 为
为![]() 外一点,且
外一点,且![]() ,仍将线段
,仍将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,
,![]() .
.
(1)![]() 的结论是否仍然成立?并请你说明理由;
的结论是否仍然成立?并请你说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)(1)见解析;(2)见解析;(Ⅱ)(1)仍然成立,见解析;(2)6.
【解析】
(Ⅰ)(1)根据旋转的性质,得到AD=AE,∠BAD=∠CAE,然后根据SAS证明全等即可;
(2)由全等的性质,得到BD=CE,然后即可得到结论;
(Ⅱ)(1)与(Ⅰ)同理,即可得到![]() ;
;
(2)根据全等的性质,得到![]() ,然后利用勾股定理求出DE,根据特殊角的三角函数值,即可求出答案.
,然后利用勾股定理求出DE,根据特殊角的三角函数值,即可求出答案.
解:(Ⅰ)(1)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,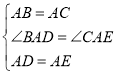 ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(Ⅱ)(1)![]() 的结论仍然成立,
的结论仍然成立,
理由:∵将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
即![]() ,
,
在![]() 与
与![]() 中,
中,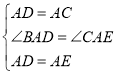 ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目