��Ŀ����
���壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ���
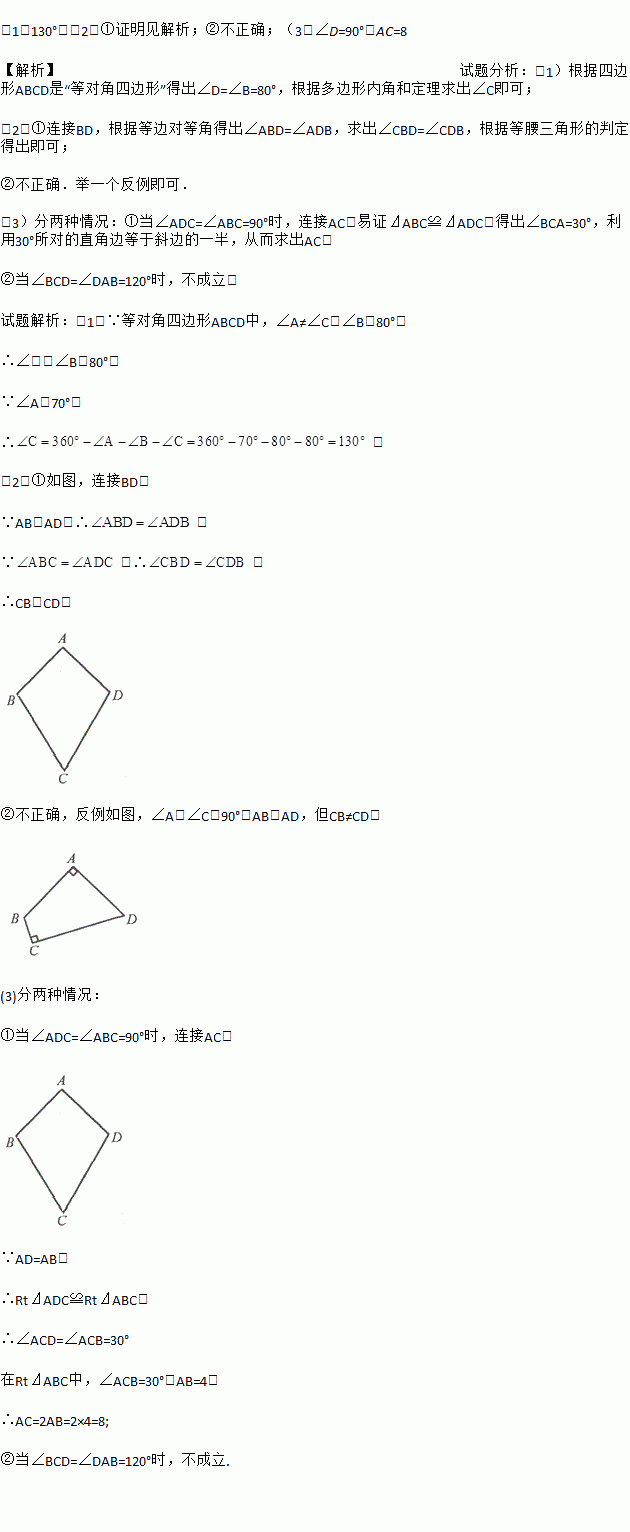
��1����֪����ͼ1���ı���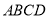 �ǡ��ȶԽ��ı��Ρ���
�ǡ��ȶԽ��ı��Ρ��� 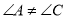 ��
�� 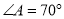 ��
�� 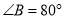 ����
����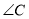 ��
�� 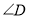 �Ķ�����
�Ķ�����
��2����̽�����ȶԽ��ı��Ρ�����ʱ��
�� С�컭��һ�����ȶԽ��ı��Ρ�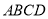 ����ͼ2��������
����ͼ2��������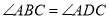 ��
�� 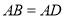 ����ʱ������
����ʱ������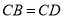 ����������֤���˽��ۣ�
����������֤���˽��ۣ�
�� �ɴ�С����룺���������⡮�ȶԽ��ı��Ρ�����һ���ڱ����ʱ����һ���ڱ�Ҳ��ȡ�������Ϊ���IJ�����ȷ������ȷ����֤����������ȷ����ٳ�������
��3����֪���ڡ��ȶԽ��ı��Ρ�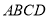 �У�
�� 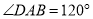 ��
��  ��AB=AD=4�������D�ͶԽ���
��AB=AD=4�������D�ͶԽ���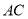 �ij���
�ij���
��ϰ��ϵ�д�
 ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�
�����Ŀ

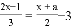 ,ȥ��ĸʱ,�����ұߵ�-3���dz�6,�������Ľ�Ϊx=2,��ԭ������ȷ�Ľ�Ϊ(��)
,ȥ��ĸʱ,�����ұߵ�-3���dz�6,�������Ľ�Ϊx=2,��ԭ������ȷ�Ľ�Ϊ(��)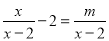 ����������m��ֵΪ__________��
����������m��ֵΪ__________��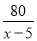 ��
��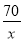 B.
B. 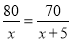 C.
C. 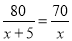 D.
D. 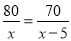
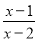 ��
��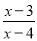 =
=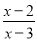 ��
��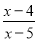 �Ľ���x=
�Ľ���x=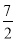 ������
������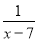 ��
��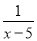 =
=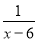 ��
��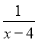 �Ľ���x=
�Ľ���x=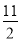 ���Բ��룺
���Բ��룺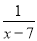 +
+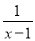 =
=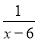 +
+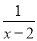 �Ľ⣻
�Ľ⣻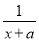 ��
��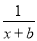 =
=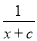 ��
��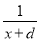 �Ľ⣨a��b��c��d��ʾ��ͬ��������
�Ľ⣨a��b��c��d��ʾ��ͬ��������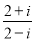 �����a+bi����ʽ��
�����a+bi����ʽ��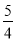 �������������ȵ�һ������30֧��
�������������ȵ�һ������30֧��