题目内容
在⊙O中,半径R=1,弦AB=| 2 |
| 3 |
分析:作垂直于弦的半径,构造直角三角形,利用三角函数的特殊值进行解答.
解答: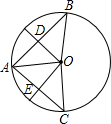 解:利用垂径定理可知:AD=
解:利用垂径定理可知:AD=
,AE=
,
根据直角三角形中三角函数的值可知:
sin∠AOD=
,
∴∠AOD=60°sin∠AOE=
,
∴∠AOE=45°,
∴∠BAC=75°.
当两弦共弧的时候就是15°.
故答案为:75°或15°.
 解:利用垂径定理可知:AD=
解:利用垂径定理可知:AD=
| ||
| 2 |
| ||
| 2 |
根据直角三角形中三角函数的值可知:
sin∠AOD=
| ||
| 2 |
∴∠AOD=60°sin∠AOE=
| ||
| 2 |
∴∠AOE=45°,
∴∠BAC=75°.
当两弦共弧的时候就是15°.
故答案为:75°或15°.
点评:本题的关键是画图,图形可以帮助学生直观简单的理清题意,然后利用垂径定理和特殊角的三角函数求解即可.注意本题有两种情况.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,在⊙O中,半径OA=2,△ABC是⊙O的内接三角形,圆周角∠ACB=60°,则弦AB的长是多少?
如图,在⊙O中,半径OA=2,△ABC是⊙O的内接三角形,圆周角∠ACB=60°,则弦AB的长是多少?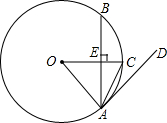 (2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.
(2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E. 如图在⊙O中,半径OB=10,弦AB=10,则弦AB所对圆周角为
如图在⊙O中,半径OB=10,弦AB=10,则弦AB所对圆周角为