Question

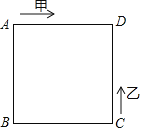
【题目】如图，将矩形ABCD沿GH对折，点C落在Q处，点D落在E处，EQ与BC相交于F．若AD=8cm，AB=6cm，AE=4cm．则△EBF的周长是 cm．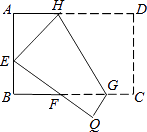

Answer 1

【答案】8
【解析】解：设AH=a，则DH=AD﹣AH=8﹣a，

在Rt△AEH中，∠EAH=90°，AE=4，AH=a，EH=DH=8﹣a，

∴EH2=AE2+AH2，即（8﹣a）2=42+a2，

解得：a=3．

∵∠BFE+∠BEF=90°，∠BEF+∠AEH=90°，

∴∠BFE=∠AEH．

又∵∠EAH=∠FBE=90°，

∴△EBF∽△HAE，

∴ = = = ．

∵C△HAE=AE+EH+AH=AE+AD=12，

∴C△EBF= C△HAE=8．

故答案为：8．

设AH=a，则DH=AD﹣AH=8﹣a，利用勾股定理求出a的值，再根据同角的余角相等得∠BFE=∠AEH，从而证出△EBF∽△HAE，根据相似三角形的周长比等于相似比（即对应边的比）即可得出结论.