题目内容
如图,A,B是海面上位于东西方向相距 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
【答案】分析:在△DAB中,由正弦定理得 ,由此可以求得DB=10
,由此可以求得DB=10 海里;然后在△DBC中,由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC=900,即CD=30海里;最后根据时间=
海里;然后在△DBC中,由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC=900,即CD=30海里;最后根据时间= 即可求得该救援船到达D点需要的时间.
即可求得该救援船到达D点需要的时间.
解答: 解:由题意知AB=5(3+
解:由题意知AB=5(3+ )海里,∠DBA=90°-60°=30°,∠DAB=45°,
)海里,∠DBA=90°-60°=30°,∠DAB=45°,
∴∠ADB=105°,
在△DAB中,由正弦定理得 ,
,
∴DB= ,
,
= ,
,
= ,
,
= ,
,
=10 (海里),
(海里),
又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20 海里,
海里,
在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD•BC•cos∠DBC
=300+1200-2×10 ×20
×20 ×
× =900,
=900,
∴CD=30(海里),则需要的时间t= =1(小时).
=1(小时).
答:救援船到达D点需要1小时.
点评:本题考查了正弦定理与余弦定理.准确找出题中的方向角是解题的关键之处.
 ,由此可以求得DB=10
,由此可以求得DB=10 海里;然后在△DBC中,由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC=900,即CD=30海里;最后根据时间=
海里;然后在△DBC中,由余弦定理得CD2=BD2+BC2-2BD•BC•cos∠DBC=900,即CD=30海里;最后根据时间= 即可求得该救援船到达D点需要的时间.
即可求得该救援船到达D点需要的时间.解答:
 解:由题意知AB=5(3+
解:由题意知AB=5(3+ )海里,∠DBA=90°-60°=30°,∠DAB=45°,
)海里,∠DBA=90°-60°=30°,∠DAB=45°,∴∠ADB=105°,
在△DAB中,由正弦定理得
 ,
,∴DB=
 ,
,=
 ,
,=
 ,
,=
 ,
,=10
 (海里),
(海里),又∠DBC=∠DBA+∠ABC=30°+(90°-60°)=60°,BC=20
 海里,
海里,在△DBC中,由余弦定理得
CD2=BD2+BC2-2BD•BC•cos∠DBC
=300+1200-2×10
 ×20
×20 ×
× =900,
=900,∴CD=30(海里),则需要的时间t=
 =1(小时).
=1(小时).答:救援船到达D点需要1小时.
点评:本题考查了正弦定理与余弦定理.准确找出题中的方向角是解题的关键之处.

练习册系列答案
相关题目
 数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据:
数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据: ,正以每小时
,正以每小时 一个正方体六个面上分别写着“东”、“海”、“实”、“验”、“学”、“校”,如图是这个正方体的三种不同的摆法,则与“东”、“海”、“实”所在面相对的面上的字分别是
一个正方体六个面上分别写着“东”、“海”、“实”、“验”、“学”、“校”,如图是这个正方体的三种不同的摆法,则与“东”、“海”、“实”所在面相对的面上的字分别是 数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据:
数学与生产实际紧密联系,经常用于军事和国防上的计算.如图是设在我国某段海防线上的两个观测站A、B,上午9点,发现海面上C处有一可疑船只,通过通讯联络,立刻测得船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、B两站的距离是50米,请你求出此时可疑船只离海岸线的距离(精确到米).(参考数据: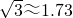 ,
,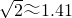 )
) ,
, )
)