Question

在△OAC中，∠AOC=90°，OB=6，BC=12，∠ABO+∠C=90°，M、N分别在线段AB、AC上．
（1）填空：cosC=______

Answer 1

【答案】分析：（1）根据相似三角形的判定得出△AOB∽△COA，进而得出AO的长，即可求出cosC的值；
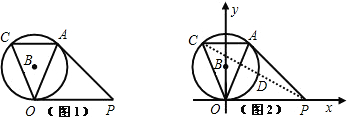
（2）利用（1）中所求得出AB=BC=12，再利用①∠AMN=∠B时，（如图1）△AMN∽△ABC，②当∠AMN=∠C时，（如图2）△AMN∽△ACB分别求出即可；
（3）首先得出△AMN∽△ABC，①当EN与线段AB相交时，设EN与AB交于点F（如图3），②当EN与线段AB不相交时，设EN于BC交于点G（如图4），分别求出即可．
解答：解：（1）∵AO⊥OC，
∴∠ABO+∠BAO=90°．
∵∠ABO+∠C=90°，
∴∠BAO=∠C．
又∵∠ABO=∠COA，
∴△AOB∽△COA．
∵OB=6，BC=12，
∴6：OA=OA：18，
∴OA=6，
∴AC===12，
∴cosC===；
故答案为：；

（2）∵cosC=，
∴∠C=30°，
∵tan∠ABO===，
∴∠ABO=60°，
∴∠BAC=30°，
∴AB=BC=12．
①∠AMN=∠B时，如图1，△AMN∽△ABC．
∵AM=4，
∴S_△AMN：S_△ABC=AM²：AB²=4²：12²=1：9．
②当∠AMN=∠C时，如图2，△AMN∽△ACB．
∵AM=4，
∴S_△AMN：S_△ABC=AM²：AC²=4²：（12）²=1：27．
故答案为：1：9或1：27；

（3）可以求得：S_△ABC=AO•BC=×6×12=36．
∵MN∥BC，
∴△AMN∽△ABC．
∴S_△AMN：S_△ABC=MN²：BC²．
∴S_△AMN：36=x²：12²．
∴S_△AMN=x²．
①当EN与线段AB相交时，设EN与AB交于点F（如图3），
∵MN∥BC，
∴∠ANM=∠C=30°．
∴∠ANM=∠BAC．
∴AM=MN=x．
∵将△AMN沿MN折叠，
∴∠ENM=∠ANM=30°．
∴∠AFN=90°．
∴MF=MN=AM=x．
∴S_△FMN：S_△AMN=MF：AM．
∴y：x²=x：x=1：2．
∴y=x²（0＜x≤6）；
②当EN与线段AB不相交时，设EN于BC交于点G（如图4），
∵MN∥BC，
∴CN：AC=BM：AB．
∴CN：12=（12-x）：12，
∴CN=12-x．
∵△CNG∽△CBA，
∴S_△CNG：S_△ABC=CN²：BC²．
∴S_△CNG：36=（12-x）²：12²．
∴S_△CNG=（12-x）²．
∴S_阴=S_△ABC-S_△AMN-S_△CNG=36-x²-（12-x）²．
即y=-x²+18x-72（6＜x＜12）．
点评：此题主要考查了相似三角形的判定与性质，根据直线EN与线段AB位置关系进行分类讨论得出是解题关键．