Question

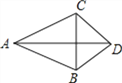
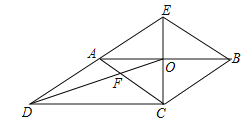
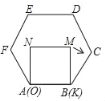
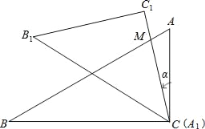
【题目】如图，是一副学生用的三角板，在△ABC 中，∠C＝90°，∠A＝60°，∠B＝30°；在△A1B1C1中，∠C1＝90°，∠B1A1 C1＝45°，∠B1＝45°，且A1B1＝CB．若将边A1C1与边CA重合，其中点A1与点C重合．将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转过的角为α，旋转过程中边A1C1与边AB的交点为M，设AC＝a．

（1）计算A1C1的长；

（2）当α＝30°时，证明：B1C1∥AB；

（3）若a＝，当α＝45°时，计算两个三角板重叠部分图形的面积；

（4）当α＝60°时，用含a的代数式表示两个三角板重叠部分图形的面积．

（参考数据：sin15°＝，cos15°＝，tan15°＝2﹣，sin75°＝，cos75°＝，tan75°＝2+）

Answer 1

【答案】（1）A1C1＝；（2）见解析；（3）两个三角板重叠部分图形的面积＝3+3；（4）两个三角板重叠部分图形的面积＝．

【解析】

（1）在Rt△ABC中，由特殊锐角三角函数值，先求得BC的长，然后在Rt△A1B1C1中利用特殊锐角三角函数即可求得A1C1的长；
（2）利用三角形的外角的性质求得∠BMC=90°，然后利用同位角相等，两直线平行进行判定即可；
（3）两个三角板重叠部分图形的面积=△A1B1C1的面积-△BC1M的面积；
（4）两个三角板重叠部分图形的面积=．

（1）在Rt△ABC中，∠B＝30°，AC＝a，

由特殊锐角三角函数可知：，

∴BC＝．

∴B1 A1＝

在Rt△A1B1C1，∠B1＝∠45°，

∴．

∴A1C1＝．

（2）∵∠ACM＝30°，∠A＝60°，

∴∠BMC＝90°．

∴∠C1＝∠BMC．

∴B1C1∥AB．

（3）如下图：

由（1）可知：A1C1＝＝＝3+

∴△A1B1C1的面积＝

∵∠A1B1C1＝45°，∠ABC＝30°

∴∠MBC1＝15°

在Rt△BC1M中，C1M＝BC1tan15°＝（3+）（2﹣）＝3﹣，

∴Rt△BC1M的面积＝＝（3+）（3﹣）＝3．

∴两个三角板重叠部分图形的面积＝△A1B1C1的面积﹣△BC1M的面积＝3+3．

（4）由（1）可知：BC＝，A1C1＝，

∴C1F＝A1C1tan30°＝a，

∴=×a×a=

∵∠MCA＝60°，∠A＝60°，

∴∠AMC＝60°

∴MC＝AC＝MA＝a．

∴C1M＝C1A1﹣MC＝．

∵∠MCA＝60°，

∴∠C1A1B＝30°，

∴∠C1MD＝∠B+∠C1A1B＝60°

在Rt△DC1M中，由特殊锐角三角函数可知：C1D＝C1Mtan60°＝a，

∴＝C1MC1D=a2，

两个三角板重叠部分图形的面积＝a2