题目内容
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD,

(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,AC=17,求CF的长.
(1)证明见解析;(2)8.
【解析】
试题分析:(1)首先利用角平分线的性质得出CF=CE,进而利用HL定理得出Rt△CFD≌Rt△CEB;
(2)首先得出Rt△CFA≌Rt△CEA,进而得出AF=AE,设DF=x,则9+x=21-x,求出x即可得出AE的长,然后利用勾股定理即可求出CF的长..
试题解析:(1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△CFD和Rt△CEB中,
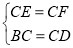 ,
,
∴Rt△CFD≌Rt△CEB(HL);
(2)【解析】
∵在Rt△CFA和Rt△CEA中,
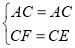 ,
,
∴Rt△CFA≌Rt△CEA(HL),
∴AF=AE,设DF=x,
则9+x=21-x,
解得:x=6,
故AE=21-6=15.
在Rt△ACF中,CF=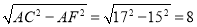 .
.
考点:全等三角形的判定与性质.

练习册系列答案
相关题目
 、
、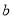 互为相反数,
互为相反数, 、
、 互为倒数,
互为倒数,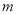 到原点的距离为2,则代数式|m|-cd+
到原点的距离为2,则代数式|m|-cd+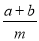 的值为 .
的值为 . 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
 的取值范围是 ;
的取值范围是 ;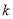 的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小? ,
, ,求双曲线的解析式.
,求双曲线的解析式. ,则AD的长为 ( )
,则AD的长为 ( )
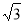 C.
C. D.1
D.1 时,原方程应变形为( )
时,原方程应变形为( ) B.
B. C.
C. D.
D.



 的结果为( )
的结果为( )