题目内容
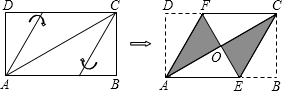
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.如果AB=
,那么BC的长为

| 3 |
1
1
.
分析:根据折叠的性质得到EA=EC,∠BCE=∠ACE,则∠ACE=∠CAE,利用三角形外角性质有∠CEB=∠CAE+∠ACE,所以∠CEB=2∠BCE,则可计算出∠BCE=30°,
所以∠CAE=30°,然后根据含30°的直角三角形三边的关系计算出BC.
所以∠CAE=30°,然后根据含30°的直角三角形三边的关系计算出BC.
解答:解:∵矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,
∴EA=EC,∠BCE=∠ACE,
∴∠ACE=∠CAE,
而∠CEB=∠CAE+∠ACE,
∴∠CEB=2∠BCE,
∴∠BCE=30°,
∴∠CAE=30°,
在Rt△ABC中,∠CAB=30°,AB=
,
∴BC=
=1.
故答案为1.
∴EA=EC,∠BCE=∠ACE,
∴∠ACE=∠CAE,
而∠CEB=∠CAE+∠ACE,
∴∠CEB=2∠BCE,
∴∠BCE=30°,
∴∠CAE=30°,
在Rt△ABC中,∠CAB=30°,AB=
| 3 |
∴BC=
| AB | ||
|
故答案为1.
点评:本题考查了折叠的性质:折叠前后两图象全等,即对应线段相等,对应角相等.也考查了含30°的直角三角形三边的关系.

练习册系列答案
相关题目
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )
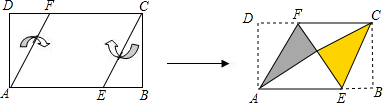

| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
 C的长为
C的长为

