题目内容
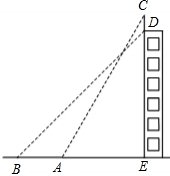 江苏省第八届园博会于2013年在我市举行,宣传部门在一幢大楼(DE)的顶部竖有一块“江魂秘境,水韵方舟”的宣传牌CD,其宽度为2m,小明在平地上的A处,测得宣传牌的顶部C的仰角为60°;又沿着EA的方向前进了22m到B处,测得宣传牌的底部D的仰角为45°(A、E之间有一条河),求这幢大楼DE的高度.(测角器的高度忽略不计,结果精确到0.1m.参考数据:
江苏省第八届园博会于2013年在我市举行,宣传部门在一幢大楼(DE)的顶部竖有一块“江魂秘境,水韵方舟”的宣传牌CD,其宽度为2m,小明在平地上的A处,测得宣传牌的顶部C的仰角为60°;又沿着EA的方向前进了22m到B处,测得宣传牌的底部D的仰角为45°(A、E之间有一条河),求这幢大楼DE的高度.(测角器的高度忽略不计,结果精确到0.1m.参考数据:| 2 |
| 3 |
分析:根据条件可以证明△DBE是等腰直角三角形,因而可以设DE=x,则BE=x,即可利用x表示出CE,AE的长度,在直角△AEC中利用三角函数即可得到关于x的方程,从而求解.
解答:解:由题意得:AB=22m,CD=2m,
∠CAE=60°,∠CBE=45°,
∵∠CBE=45°而CE⊥BE,
∴DE=BE.
设DE=xm,则CE=x+2m,
∴AE=BE-AB=x-22m
∴在Rt△DAE中,tan∠CAE=
,
∴
=
,
解得:x=(11
+1)(
+1)≈44.0m.
答:这幢大楼DE的高度44.0m.

∠CAE=60°,∠CBE=45°,
∵∠CBE=45°而CE⊥BE,
∴DE=BE.
设DE=xm,则CE=x+2m,
∴AE=BE-AB=x-22m
∴在Rt△DAE中,tan∠CAE=
| CE |
| AE |
∴
| 3 |
| x+2 |
| x-22 |
解得:x=(11
| 3 |
| 3 |
答:这幢大楼DE的高度44.0m.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形,并且利用了方程思想.

练习册系列答案
相关题目
 实践应用
实践应用 1.414,
1.414, 1.732)
1.732)
 江苏省第八届园博会于2013年在我市举行,宣传部门在一幢大楼(DE)的顶部竖有一块“江魂秘境,水韵方舟”的宣传牌CD,其宽度为2m,小明在平地上的A处,测得宣传牌的顶部C的仰角为60°;又沿着EA的方向前进了22m到B处,测得宣传牌的底部D的仰角为45°(A、E之间有一条河),求这幢大楼DE的高度.(测角器的高度忽略不计,结果精确到0.1m.参考数据:
江苏省第八届园博会于2013年在我市举行,宣传部门在一幢大楼(DE)的顶部竖有一块“江魂秘境,水韵方舟”的宣传牌CD,其宽度为2m,小明在平地上的A处,测得宣传牌的顶部C的仰角为60°;又沿着EA的方向前进了22m到B处,测得宣传牌的底部D的仰角为45°(A、E之间有一条河),求这幢大楼DE的高度.(测角器的高度忽略不计,结果精确到0.1m.参考数据: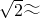 1.414,
1.414, 1.732)
1.732) 1.414,
1.414, 1.732)
1.732)