题目内容
 如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于C、D,交AB于E,AF为⊙O的直径,有下列结论:
①∠ABP=∠AOP;② =
= ;③AC平分∠PAB;④2BE2=PE•BF,
;③AC平分∠PAB;④2BE2=PE•BF,
其中结论正确的有
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:首先连接OB,根据切线长定理得PA=PB,∠APO=∠BPO;易证得△APO≌△BPO,得∠AOP=∠BOP,即 =
= ;再根据这些基础条件进行判断.
;再根据这些基础条件进行判断.
解答: 解:连接OB;
解:连接OB;
∵PA、PB都是⊙O的切线,
∴PA=PB,∠APO=∠BPO;
又PO=OP,
∴△APO≌△BPO,
∴∠AOP=∠BOP,
∴ =
= ;
;
①∵PB切⊙O于点B,
∴∠PBA=∠AFB,
由 =
= ,得∠AFB=∠AOP,
,得∠AFB=∠AOP,
∴∠PBA=∠AOP;
故①正确;
②∵∠AOC=∠BOC=∠FOD,
∴ =
= =
=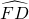 ;
;
故②正确;
③同①,可得∠PAB=∠AOC;
∵ =
= ,
,
∴∠AOC=∠BOC,
∴∠EAC= ∠BOC=
∠BOC= ∠AOC,
∠AOC,
∴∠EAC= ∠PAB,
∠PAB,
∴AC平分∠PAB;故③正确;
④在△PEB和△ABF中,
 ,
,
∴△PEB∽△ABF,
∴BE:PE=BF:AB=BF:2BE,即2BE2=PE•BF,
故④正确;
综上所述,正确的结论共有4个;
故选D.
点评:此题主要考查的是切线的性质,涉及的知识点有:圆周角定理,全等三角形的判断和性质,切线长定理,圆心角、弧、弦的关系等.
分析:首先连接OB,根据切线长定理得PA=PB,∠APO=∠BPO;易证得△APO≌△BPO,得∠AOP=∠BOP,即
 =
= ;再根据这些基础条件进行判断.
;再根据这些基础条件进行判断.解答:
 解:连接OB;
解:连接OB;∵PA、PB都是⊙O的切线,
∴PA=PB,∠APO=∠BPO;
又PO=OP,
∴△APO≌△BPO,
∴∠AOP=∠BOP,
∴
 =
= ;
;①∵PB切⊙O于点B,
∴∠PBA=∠AFB,
由
 =
= ,得∠AFB=∠AOP,
,得∠AFB=∠AOP,∴∠PBA=∠AOP;
故①正确;
②∵∠AOC=∠BOC=∠FOD,
∴
 =
= =
=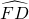 ;
;故②正确;
③同①,可得∠PAB=∠AOC;
∵
 =
= ,
,∴∠AOC=∠BOC,
∴∠EAC=
 ∠BOC=
∠BOC= ∠AOC,
∠AOC,∴∠EAC=
 ∠PAB,
∠PAB,∴AC平分∠PAB;故③正确;
④在△PEB和△ABF中,
 ,
,∴△PEB∽△ABF,
∴BE:PE=BF:AB=BF:2BE,即2BE2=PE•BF,
故④正确;
综上所述,正确的结论共有4个;
故选D.
点评:此题主要考查的是切线的性质,涉及的知识点有:圆周角定理,全等三角形的判断和性质,切线长定理,圆心角、弧、弦的关系等.

练习册系列答案
相关题目
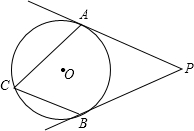 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
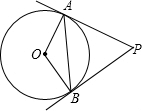 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于