题目内容
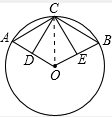
 如图在⊙O中,AC=BC,OD=OE,求证:∠ACD=∠BCE.
如图在⊙O中,AC=BC,OD=OE,求证:∠ACD=∠BCE.
解:连接OC,
∵AC=BC,
∴ ∠AOC=∠BOC,
∠AOC=∠BOC,
∵在△AOC和△BOC中,
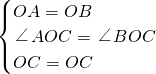 ,
,
∴△AOC≌△BOC(SAS),
∴∠A=∠B,
∵OD=OE,
∴AD=BE,
∵在△ACD和△BCE中,
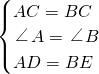 ,
,
∴△ACD≌△BCE(SAS),
∴∠ACD=∠BCE.
分析:先连接OC,根据SAS证出△AOC≌△BOC,得出∠A=∠B,再根据OD=OE,得出AD=BE,然后根据SAS证出△ACD≌△BCE,从而得出∠ACD=∠BCE.
点评:此题考查了圆心角、弧、弦的关系,用到的知识点是全等三角形的判定与性质,关键是做出辅助线,构造全等三角形.
∵AC=BC,
∴
 ∠AOC=∠BOC,
∠AOC=∠BOC,∵在△AOC和△BOC中,
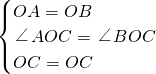 ,
,∴△AOC≌△BOC(SAS),
∴∠A=∠B,
∵OD=OE,
∴AD=BE,
∵在△ACD和△BCE中,
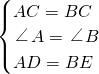 ,
,∴△ACD≌△BCE(SAS),
∴∠ACD=∠BCE.
分析:先连接OC,根据SAS证出△AOC≌△BOC,得出∠A=∠B,再根据OD=OE,得出AD=BE,然后根据SAS证出△ACD≌△BCE,从而得出∠ACD=∠BCE.
点评:此题考查了圆心角、弧、弦的关系,用到的知识点是全等三角形的判定与性质,关键是做出辅助线,构造全等三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
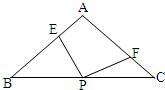 30、如图在△ABC中AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F.
30、如图在△ABC中AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F. 16、如图在△ABC中,AC=7,DE是AB的垂直平分线,若BC=5,△BCE的周长是
16、如图在△ABC中,AC=7,DE是AB的垂直平分线,若BC=5,△BCE的周长是 19、已知:如图在?ABCD中,AC,BD交于O,CE⊥BD于E,AF⊥BD于F,连接AE,CF.
19、已知:如图在?ABCD中,AC,BD交于O,CE⊥BD于E,AF⊥BD于F,连接AE,CF.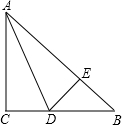 如图在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,CD=4cm.求AC的长是多少厘米.
如图在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,CD=4cm.求AC的长是多少厘米.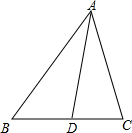 如图在△ABC中,AC=AD=BC,∠B=50°,那么∠C=
如图在△ABC中,AC=AD=BC,∠B=50°,那么∠C=