题目内容
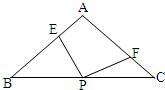30、如图在△ABC中AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB、AC于点E、F．（1）求证：AE=CF（提示：添辅助线）
（2）是否还有其他结论，不要求证明（至少2个）
分析：连接AP，证明△APE≌△CFP，利用直角∠EPF和直角∠APC可证，然后利用全等三角形的性质就可以证明题目结论．
解答：
证明：（1）连接AP，
∵AB=AC，∠BAC=90°，P是BC的中点，
∴∠BAP=∠CAP=∠ACB=45°，CP=AP，
而∠EPF=90°，∠APC=90°，
∴∠APE=∠FPC，
∴△APE≌△CFP．
∴AE=CF．
（2）BE=AF，EP=PF等等．
证明：（1）连接AP，∵AB=AC，∠BAC=90°，P是BC的中点，
∴∠BAP=∠CAP=∠ACB=45°，CP=AP，
而∠EPF=90°，∠APC=90°，
∴∠APE=∠FPC，
∴△APE≌△CFP．
∴AE=CF．
（2）BE=AF，EP=PF等等．
点评：此题主要考查了等腰直角三角形的性质，利用其对应边相等，对应角相等解题．
练习册系列答案
相关题目
