题目内容
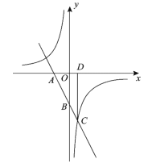
【题目】如图,以![]() 为顶点的抛物线
为顶点的抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 的表达式为
的表达式为![]() .
.
(1)求抛物线的表达式;
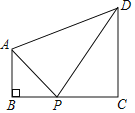
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上有一点
上有一点![]() ,若使
,若使![]() 的值最小,则点
的值最小,则点![]() 的坐标为____________.
的坐标为____________.
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3)![]() .
.
【解析】
(1)通过![]() 的表达式为
的表达式为![]() 求解出B、C点的坐标,利用待定系数法得到方程组,进而求出抛物线方程所含的未知数,得到抛物线的表达式;
求解出B、C点的坐标,利用待定系数法得到方程组,进而求出抛物线方程所含的未知数,得到抛物线的表达式;
(2)通过做垂线DF,交BC于E,求![]() 的面积可转化成求
的面积可转化成求![]() 和
和![]() 的面积之和,即可求解;
的面积之和,即可求解;
(3)作点O关于BC的对称点,利用对称点的性质,可以把![]() 的最小值转化成
的最小值转化成![]() 的最小值进而求得直线
的最小值进而求得直线![]() 的解析式,联立直线BC的解析式得到方程组,通过解方程组求出
的解析式,联立直线BC的解析式得到方程组,通过解方程组求出![]() 的坐标.
的坐标.
解:(1)把![]() 代入
代入![]() ,得:
,得:![]() ,
,
![]() .
.
把![]() 代入
代入![]() ,得:
,得:![]() ,
,
![]() .
.
把![]() 代入
代入![]() ,
,
得:![]() ,
,
解得![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
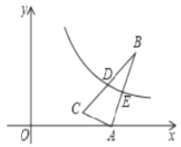
(2)如下图,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]()
![]() ,
,
![]() 顶点
顶点![]() .
.
当![]() 时,
时,![]() ,
,
![]() ,即
,即![]() .
.
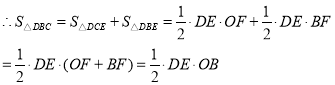
由(1)知:![]() ,即
,即![]() ,
,
![]() .
.
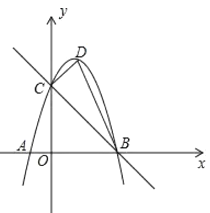
(3)如下图,作点O关于BC的对称点![]() ,由
,由![]() ,则
,则![]()
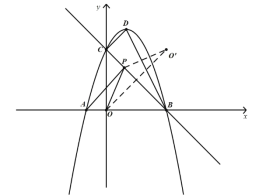
∵O与![]() 关于BC对称,∴
关于BC对称,∴![]() ,
,
∴![]() 的最小值=
的最小值=![]() 的最小值=
的最小值=![]() =
=![]() (两点之间线段最短),
(两点之间线段最短),
由A(-1,0)、![]() ,求得直线
,求得直线![]() 的解析式是
的解析式是![]() ,
,
联立直线![]() 的表达式
的表达式![]() ,
,
P点坐标满足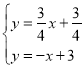 ,
,
解得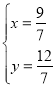 ,
,
所以![]() .
.

练习册系列答案
相关题目