题目内容
如图CE是等边三角形ABC边AB边上的高，AB=4，DA⊥AB，DA=
,BD与CE、CA分别交于点F、M .（1）求CF的长；（2）求△ABM的面积。
解：（1）∵CE是等边三角形ABC边AB上的高
∴E是AB的中点
又∵DA⊥AB
∴CE∥DA
∵DA=
∴EF
∵AB=4
∴CE
∴
（2）解法一：如图1，过点M作MN⊥AB于点N
∵△ADM∽△CFM
∴
∴
在直角三角形AMN中
∵
，∠MAB=60°
∴
∴△ABM的面积
解法二：如图2，过点D作AD的垂线交AC于点G
∵∠BAC=60°，DA⊥AB
∴∠DAG=30°
在直角三角形ADG中，AD=
∴DG=1，AG=2
∵DG∥AB
∴△GDM∽△ABM
∴
∴
过点M作MN⊥AB于点N
在直角三角形AMN中
∵，∠MAB=60°
∴
∴△ABM的面积
解法三：以AB所在直线为
轴，E为坐标原点，建立如图3所示的平面直角 坐标系，由题意知：点A、B、C、D的坐标为（－2，0）、（2，0）、（0，
）、（－2，）
∴直线BD的解析式为
∴直线AC的解析式为
∴两直线的交点M的坐标为（
，
）
∵AB=4
∴△ABM的面积
练习册系列答案
阅读快车系列答案
相关题目
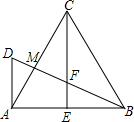如图CE是等边三角形ABC边AB边上的高，AB=4，DA⊥AB，DA=
，BD与CE、CA分别交于点F、M．
，BD与CE、CA分别交于点F、M．
，BD与CE、CA分别交于点F、M．