题目内容
 如图,半圆O的直径AB=2,四边形COAD为正方形,连接AC,若正方形内三部分的面积分别记为S1,S2,S3,则S1:S2:S3=________.
如图,半圆O的直径AB=2,四边形COAD为正方形,连接AC,若正方形内三部分的面积分别记为S1,S2,S3,则S1:S2:S3=________.
(4-π):(π-2):2
分析:根据正方形面积计算公式求正方形COAD的面积,根据直角三角形面积计算公式求S3,根据扇形的面积计算公式求S2.
解答:由题意知OB=OA=1,
正方形COAD的面积=1×1=1,
S3= ×1×1=
×1×1= ,
,
S2= ×π×1×1-S3=
×π×1×1-S3= ,
,
S1=1-S2-S3=1-( )-
)- =1-
=1- .
.
S1:S2:S3=( ):(
):( ):(
):( )
)
整理得S1:S2:S3=(4-π):(π-2):2,
故答案为 (4-π):(π-2):2.
点评:本题考查了扇形,正方形,直角三角形的面积计算方法,考查了正方形各边均相等的性质,本题准确计算S1、S2、S3是解本题的关键.
分析:根据正方形面积计算公式求正方形COAD的面积,根据直角三角形面积计算公式求S3,根据扇形的面积计算公式求S2.
解答:由题意知OB=OA=1,
正方形COAD的面积=1×1=1,
S3=
 ×1×1=
×1×1= ,
,S2=
 ×π×1×1-S3=
×π×1×1-S3= ,
,S1=1-S2-S3=1-(
 )-
)- =1-
=1- .
.S1:S2:S3=(
 ):(
):( ):(
):( )
)整理得S1:S2:S3=(4-π):(π-2):2,
故答案为 (4-π):(π-2):2.
点评:本题考查了扇形,正方形,直角三角形的面积计算方法,考查了正方形各边均相等的性质,本题准确计算S1、S2、S3是解本题的关键.

练习册系列答案
相关题目
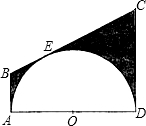 如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.
如图,半圆O的直径AD=12cm,AB,BC,CD分别与半圆O切于点A,E,D.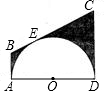 如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
如图,半圆O的直径AD=12cm,AB、BC、CD分别与半圆O切于点A、E、D.
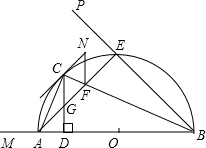 N∥CD,过C作圆的切线交FN于N.
N∥CD,过C作圆的切线交FN于N. 如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( )
如图,半圆O的直径为6cm,∠BAC=30°,则阴影部分的面积是( ) 如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.
如图,半圆O的直径AB=20,将半圆O绕点B顺针旋转45°得到半圆O′,与AB交于点P.