题目内容
△ABC中∠C=Rt∠,有一点既在BC的对称轴上,又在AC对称轴上,则该点一定是
- A.C点
- B.BC中点
- C.AC中点
- D.AB中间
D
试题分析:设该点为O,根据轴对称图形的性质可得OB=OC,OA=OC,则OB= OA,即可得到结果。
设该点为O,
∵点O既在BC的对称轴上,又在AC对称轴上,
∴OB=OC,OA=OC,
∴OB= OA=OC,
∵∠C=Rt∠,直角三角形斜边中线等于斜边的一半,
∴点O一定是AB中点,
故选D.
考点:本题考查的是轴对称图形的性质
点评:解答本题的关键是熟练掌握轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴
试题分析:设该点为O,根据轴对称图形的性质可得OB=OC,OA=OC,则OB= OA,即可得到结果。
设该点为O,
∵点O既在BC的对称轴上,又在AC对称轴上,
∴OB=OC,OA=OC,
∴OB= OA=OC,
∵∠C=Rt∠,直角三角形斜边中线等于斜边的一半,
∴点O一定是AB中点,
故选D.
考点:本题考查的是轴对称图形的性质
点评:解答本题的关键是熟练掌握轴对称图形的定义:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴

练习册系列答案
相关题目
 如图,在△ABC中∠ACB=Rt∠,CD⊥AB于点D,已知AD=2,DB=1,则( )
如图,在△ABC中∠ACB=Rt∠,CD⊥AB于点D,已知AD=2,DB=1,则( )| A、CD=2 | ||
B、CD=
| ||
| C、AC=6 | ||
D、AC=
|
 的路径运动,且速度为每秒2㎝,设运动的时间为t秒
的路径运动,且速度为每秒2㎝,设运动的时间为t秒
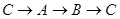 的路径运动,且速度为每秒2㎝,设运动的时间为t秒
的路径运动,且速度为每秒2㎝,设运动的时间为t秒
 的路径运动,且速度为每秒1㎝,设出发的时间为t秒.
的路径运动,且速度为每秒1㎝,设出发的时间为t秒.
 的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
的路径运动,且速度为每秒2㎝,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动。当t为何值时,直线PQ把△ABC的周长分成相等的两部分?