题目内容
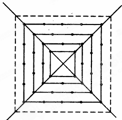 如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.
如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.
(1)填写下表:
| 层 数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 各层对应的点数 | ______ | ______ | ______ | ______ | ______ | ______ |
| 所有层的总点数 | ______ | ______ | ______ | ______ | ______ | ______ |
(2)写出第n层对应的点数;
(3)写出n层的四边形点阵的总点数;
(4)如果某一层共有79个点,你知道它是第几层吗?
(5)有没有n层的四边形点阵的总点数是180?如果有求出n,若没有说明理由.
解:(1)填表如下:
| 层数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 各层对应的点数 | 4 | 8 | 12 | 16 | 20 | 24 |
| 所有层的总点数 | 4 | 12 | 24 | 40 | 60 | 84 |
(2)由以上数据可知,第1层点数为4=4×1,
第2层点数为8=4×2,
第3层点数为12=4×3,
…,
所以,第n层所对应的点数为4n;
(3)n层的四边形点阵的总点数为:4×1+4×2+4×3+…+4n,
=4(1+2+3+…+n),
=4× ,
,
=2n(n+1);
(4)若4n=79,
则n不是整数,
所以,没有一层是79个点;
(5)若2n(n+1)=180,则n=9,
所以,前9层点数之和为180.
分析:(1)根据图形查出点数即可;
(2)根据(1)中各层点数的变化规律写出第n层的点数即可;
(3)根据各层的点数列出算式,再根据求和公式列式计算即可;
(3)把点数代入第n层的点数表达式计算即可得解;
(4)把180代入第n层的点数表达式计算即可判断.
点评:本题是对图形变化规律的考查,准确识图找出点数与层数的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
(1)填写下表:
| 层次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 该层对应的点数 | ||||||
| 所有层的总点数 |
(3)写出六边形的点阵共有n层时的总点数;
(4)如果六边形的点阵共有n层时的总点数为397,你知道共有多少层吗?
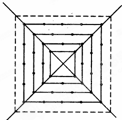 如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.
如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推. 如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推
如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推