Question

抛物线y=ax²与直线x=1，x=2，y=1，y=2组成的正方形有公共点，则a的取值范围是

 

．

Answer 1

分析：建立平面直角坐标系，画出四条直线围成的正方形，进一步判定其开口方向，再代入点的坐标即可解答．

解答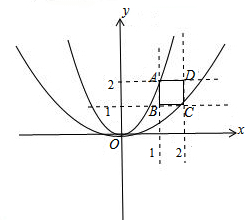：解：如图，
四条直线x=1，x=2，y=1，y=2围成正方形ABCD，
因为抛物线与正方形有公共点，所以可得a＞0，而且a值越大，抛物线开口越小，
因此当抛物线分别过A（1，2），C（2，1）时，
a分别取得最大值与最小值，代入计算得出：a=2，a=

1

4

；
由此得出a的取值范围是

1

4

≤a≤2．
故填

1

4

≤a≤2．

点评：此题利用数形结合的思想，考查了二次函数最值问题以及抛物线开口方向与a值的关系．