题目内容
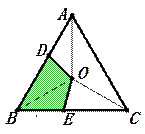
 如图,已知点O是等边三角形ABC的∠BAC、∠ACB的平分线的交点,以O为顶点作∠DOE=120°,其两边分别交AB、BC于D、E,则四边形DBEO的面积与三角形ABC的面积之比是
如图,已知点O是等边三角形ABC的∠BAC、∠ACB的平分线的交点,以O为顶点作∠DOE=120°,其两边分别交AB、BC于D、E,则四边形DBEO的面积与三角形ABC的面积之比是1:3
1:3
.分析:延长CO交AB于点M,延长AO交BC于点N,利用全等三角形的判定可知△DOM≌△EON,继而得出S四边形DBEO=S四边形MBNO=
S△ABC.
| 1 |
| 3 |
解答:解:延长CO交AB于点M,延长AO交BC于点N,如下图所示:

∵△ABC为等边三角形,O是∠BAC、∠ACB的平分线的交点,
∴O点为△ABC的中心,
∴OM⊥AB,ON⊥BC,OM=ON,∠MON=120°,
又∠DOE=120°,
∴∠DOM=∠EON,
∴△DOM≌△EON(ASA),
∴S四边形DBEO=S四边形MBNO=
S△ABC.
故答案为:1:3.

∵△ABC为等边三角形,O是∠BAC、∠ACB的平分线的交点,
∴O点为△ABC的中心,
∴OM⊥AB,ON⊥BC,OM=ON,∠MON=120°,
又∠DOE=120°,
∴∠DOM=∠EON,
∴△DOM≌△EON(ASA),
∴S四边形DBEO=S四边形MBNO=
| 1 |
| 3 |
故答案为:1:3.
点评:本题考查面积及等积变换的问题,解题关键是准确作出辅助线,得出S四边形DBEO=S四边形MBNO,难度一般.

练习册系列答案
相关题目
 8、如图,已知点O是等边△ABC三条高的交点,现将△AOB绕点O至少要旋转几度后与△BOC重合( )
8、如图,已知点O是等边△ABC三条高的交点,现将△AOB绕点O至少要旋转几度后与△BOC重合( )