Question

【题目】已知点和点在抛物线上．

（Ⅰ）求该抛物线的解析式和顶点坐标，并求出的值；

（Ⅱ）求点关于轴对称点的坐标，并在轴上找一点，使得最短，求此时点的坐标；

（Ⅲ）平移抛物线，记平移后点的对应点为，点的对应点为，点是轴上的定点．

①当抛物线向左平移到某个位置时，最短，求此时抛物线的解析式；

②是轴上的定点，当抛物线向左平移到某个位置时，四边形的周长最短，求此时抛物线的解析式（直接写出结果即可）

Answer 1

【答案】（Ⅰ），顶点坐标为，；（Ⅱ）的坐标是；（Ⅲ）①；②．

【解析】

（Ⅰ）把(-4，8)代入y=ax2可求得a的值，把x=2代入所求的抛物线解析式，可得n的值，根据二次函数的性质可得定点坐标；

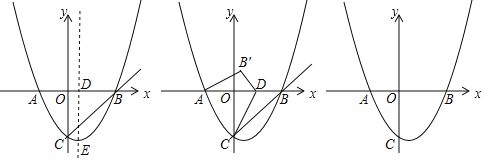
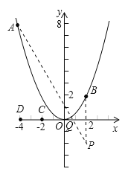
（Ⅱ）由点的坐标，得点关于轴的对称点的坐标为．连接AP交x轴于点Q，此时最短，用待定系数法求出直线AP的解析式，求得AP与x轴的交点即为Q的坐标；

（Ⅲ）①A′C+CB′最短，说明抛物线向左平移了线段CQ的距离，根据平移的规律即可求出平移后的解析式；

②设抛物线向左平移了b个单位，则点A′和点B′的坐标分别为A′(-4-b，8)和B′(2-b，2)．将点B′向左平移2个单位得B′′(-b，2)，点A′关于x轴对称点的坐标为A′′(-4-b，-8)，用含b的代数式表示出直线A′′B′′的解析式，将点D(-4，0)代入直线A′′B′′的解析式，求出b即可．

解：（Ⅰ）∵点在抛物线上，

得，解得，

∴该抛物线的解析式为，

∴抛物线的顶点坐标为．

∵点在抛物线上，

得．

（Ⅱ）由点的坐标，得点关于轴的对称点的坐标为．连接AP交x轴于点Q，此时最短，

设直线的解析式为，

则解得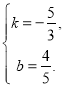

∴直线的解析式是．

令，得，

∴点的坐标是．

根据“两点之间，线段最短” 此时点满足题意．

（Ⅲ）①，

故将抛物线向左平移个单位长度时，最短．

此时抛物线的解析式为．

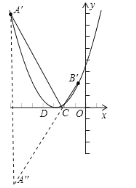
②∵线段A′B′和CD的长是定值，

∴要使四边形A′B′CD的周长最短，只要使A′D+CB′最短；

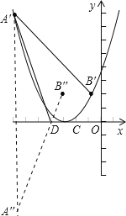
设抛物线向左平移了b个单位，

则点A′和点B′的坐标分别为A′(-4-b，8)和B′(2-b，2)．

∵CD=2，

∴将点B′向左平移2个单位得B′′(-b，2)，要使A′D+CB′最短，只要使A′D+DB′′最短，

点A′关于x轴对称点的坐标为A′′(-4-b，-8)，

设直线A′′B′′的解析式为y=mx+n，

则，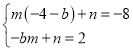

∴m=，n=b+2，

∴直线A′′B′′的解析式为y=x+b+2．

要使A′D+DB′′最短，点D应在直线A′′B′′上，

将点D(-4，0)代入直线A′′B′′的解析式，

-10+b+2=0，

解得b=，

∴将抛物线向左平移时，存在某个位置，使四边形A′B′CD的周长最短，

此时抛物线的函数解析式为y=(x+)2．