题目内容
如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.
(1)若OC=5,AB=8,求tan∠BAC;
(2)若∠DAC=∠BAC,且点D在⊙O的外部,判断直线AD与⊙O的位置关系,并加以证明.

考点:
切线的判定;勾股定理;垂径定理.
专题:
计算题.
分析:
(1)根据垂径定理由半径OC垂直于弦AB,AE=AB=4,再根据勾股定理计算出OE=3,则EC=2,然后在Rt△AEC中根据正切的定义可得到tan∠BAC的值;
(2)根据垂径定理得到AC弧=BC弧,再利用圆周角定理可得到∠AOC=2∠BAC,由于∠DAC=∠BAC,所以∠AOC=∠BAD,利用∠AOC+∠OAE=90°即可得到∠BAD+∠OAE=90°,然后根据切线的判定方法得AD为⊙O的切线.
解答:
解:(1)∵半径OC垂直于弦AB,
∴AE=BE=AB=4,
在Rt△OAE中,OA=5,AE=4,
∴OE=![]() =3,
=3,
∴EC=OC﹣OE=5﹣3=2,
在Rt△AEC中,AE=4,EC=2,
∴tan∠BAC=![]() ==;
==;
(2)AD与⊙O相切.理由如下:
∵半径OC垂直于弦AB,
∵AC弧=BC弧,
∴∠AOC=2∠BAC,
∵∠DAC=∠BAC,
∴∠AOC=∠BAD,
∵∠AOC+∠OAE=90°,
∴∠BAD+∠OAE=90°,
∴OA⊥AD,
∴AD为⊙O的切线.
点评:
本题考查了切线的判定定理:过半径的外端点且与半径垂直的直线为圆的切线.也考查了勾股定理以及垂径定理、圆周角定理.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
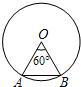 19、如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB=
19、如图,在⊙O中,半径为5,∠AOB=60°,则弦长AB=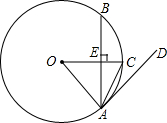 (2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E.
(2013•平凉)如图,在⊙O中,半径OC垂直于弦AB,垂足为点E. (2013•武汉模拟)如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,则圆周角∠ADC=
(2013•武汉模拟)如图,在⊙O中,半径OA⊥弦BC,∠AOB=50°,则圆周角∠ADC=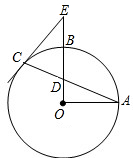 如图,在⊙O中,半径OA⊥OB,弦AC交OB于点D,E是OB延长线上一点,如果∠OAD=30°,ED=CE.
如图,在⊙O中,半径OA⊥OB,弦AC交OB于点D,E是OB延长线上一点,如果∠OAD=30°,ED=CE.