题目内容
如图1、四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线AC折叠,使点B落在D处,AD交OC于E,
(1)求OE的长;
(2)求过O、D、C三点抛物线的解析式;
(3)如图2过D做矩形DFGH,FG在x轴上,H在(2)中的抛物线上,求矩形DFGH的面积S是多少?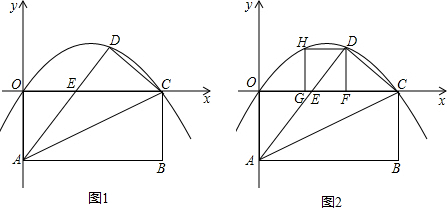
 解:(1)∵四边形OABC是矩形,
解:(1)∵四边形OABC是矩形,∴∠CDE=∠AOE=90°,OA=BC=CD.
又∵∠CED=∠OEA,
在△CDE和△AOE中,
 ,
,∴△CDE≌△AOE(AAS).
∴OE=DE.
∴OE2+OA2=(AD-DE)2,
即OE2+42=(8-OE)2,
解之,得OE=3.
(2)由(1)得出:EC=8-3=5.
如图1,过D作DG⊥EC于G,
∵∠DGE=∠CDE,∠DEG=∠CED,
∴△DGE∽△CDE.
∴
 =
=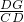 ,
,∴DG=
 ,EG=
,EG= .
.∴D(
 ,
, ).
).因为O点为坐标原点,
故可设过O,C,D三点抛物线的解析式为y=ax2+bx.
∴
 ,
,解之,得
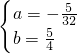 ,
,∴抛物线的解析式为:y=-
 x2+
x2+ x;
x;(3)∵C点坐标为:(8,0),
∴对称轴为:直线x=4,
∵D(
 ,
, ),
),∴H点与D点关于直线x=4对称,
∴H点坐标为;(
 ,
, ),
),∴HD=
 -
- =
= ,
,∴矩形DFGH的面积S为:DF×DH=
 ×
× =
= .
.分析:(1)已知四边形OABC是矩形,证明△CDE≌△AOE推出OE2+OA2=(AD-DE)2求出OE.
(2)本题要借助辅助线的帮助,证明∴△DGE∽△CDE,根据线段比求出DG,EG以及点D的坐标,列出解析式求出a,b的值.
(3)根据C点坐标得出抛物线的对称轴,再利用D点坐标得出H点坐标,进而得出DH,DF的长即可得出答案.
点评:此题主要考查了二次函数的综合应用以及翻折变换的性质和全等三角形的判定与性质和相似三角形的判定与性质等知识,根据已知得出D点坐标是解题关键.

练习册系列答案
相关题目
 21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1
21、已知:如图,在Rt△OAB中,∠OAB=90°,OA=AB=6cm,将△OAB绕点O沿逆时针方向旋转90°得到Rt△OA1B1 (2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.
(2011•台州模拟)如图等腰三角形纸片OAB,现要求在纸片上截一个正方形,使它的面积尽可能大.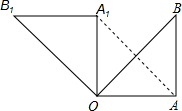 到△OA1B1.
到△OA1B1. 如图所示,△OAB绕点O旋转l80°得到△OCD,连接AD,BC,得到四边形ABCD.
如图所示,△OAB绕点O旋转l80°得到△OCD,连接AD,BC,得到四边形ABCD. (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.