题目内容
如图，在直角坐标系内有两点A（-1，1）、B（3，3），若M为x轴上一点，且MA+MB最小，并确定M点的坐标．分析：利用对称点求最短路径问题得出B′（3，-3），进而得出直线AB′的解析式即可得出答案．
解答：
解：作B点关于x轴的对称点B′点，连接AB′，直线AB′与x轴的交点即为M的坐标，
∵B（3，3），∴B′（3，-3），
将A，B′两点代入y=kx+b得：
，
解得：
，
∴直线AB′的解析式为：y=-x，
∴直线AB′y=-x，与x轴交点坐标为：（0，0）．
即M点坐标为：（0，0）．
解：作B点关于x轴的对称点B′点，连接AB′，直线AB′与x轴的交点即为M的坐标，∵B（3，3），∴B′（3，-3），
将A，B′两点代入y=kx+b得：
|
解得：
|
∴直线AB′的解析式为：y=-x，
∴直线AB′y=-x，与x轴交点坐标为：（0，0）．
即M点坐标为：（0，0）．
点评：此题主要考查了利用对称点求最短路径问题，得出B点对称点B′的位置是解题关键．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
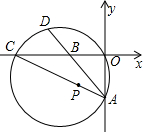AB的延长线交于点D，弧CD=弧AO，如果AB=10，AO＞BO，且AO、BO是x的二次方程x2+kx+48=0的两个根．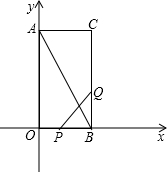
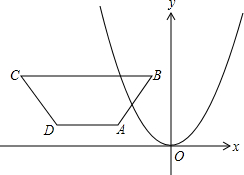
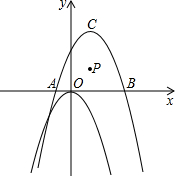（2007•西城区二模）如图，在直角坐标系内有点P（1，1）、点C（1，3）和二次函数y=-x2．
如图，在直角坐标系内，O为坐标原点，点A的坐标为（1，0），点B在x轴上且在点A的右端，OA=AB，分别过点A、B作x轴的垂线，与二次函数y=x2的图象交于C、D两点，分别过点C、D作y轴的垂线，交y轴于点E、F，直线CD交y轴于点H．