题目内容
如图,在直角坐标系内,过点C(3,6)分别作x轴和y轴的垂线CB和CA,垂足分别为B和A,点P从点O沿OB向B以1个长度单位/秒的速度运动,点Q从点B沿BC向C以2个长度单位/秒的速度运动.如果P、Q分别从O、B同时出发,运动时间为t,试求:(1)t为何值时,△PBQ的面积等于2个平方单位;
(2)若P、B、Q三点构成的三角形与A、B、C三点构成的三角形相似,求此时P和Q点的坐标.
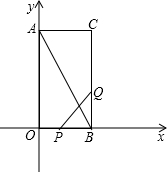
分析:(1)可设OP=t,BQ=2t,则有PB=OB-OP=3-t.根据三角形的面积公式得出关于t的方程,即可求出此时t的值;
(2)分为①若△PBQ∽△ACB;②若△PBQ∽△BCA两种情况,根据相似三角形的性质即可求出P和Q点的坐标.
(2)分为①若△PBQ∽△ACB;②若△PBQ∽△BCA两种情况,根据相似三角形的性质即可求出P和Q点的坐标.
解答:解:(1)根据题意有OB=3,BC=6
∵OP=t,BQ=2t
∴PB=OB-OP=3-t(2分)
∴S△PBQ=
PB•BQ=
•2t(3-t)=-t2+3t
当S△PBQ=2时,-t2+3t=2,即t2-3t+2=0(t-1)(t-2)=0
∴t1=1,t2=2(4分)
∴当t=1或t=2时,△PBQ的面积等于2个平方单位.
(2)∵∠ACB=∠PBQ=90°
①若△PBQ∽△ACB
则
=
即
=
∴t=
此时P点坐标为P(
,0),Q点坐标为Q(3,3)(7分)
②若△PBQ∽△BCA
则
=
即
=
∴t=
此时P点坐标为P(
,0),Q点坐标为Q,3,
)(10分)
∴若P、B、Q三点构成的三角形与A、B、C三点构成的三角形相似,此时P和Q
点的坐标分别为P(
,0),Q(3,3)或P(
,0),Q(3,
,3).
∵OP=t,BQ=2t
∴PB=OB-OP=3-t(2分)
∴S△PBQ=
| 1 |
| 2 |
| 1 |
| 2 |
当S△PBQ=2时,-t2+3t=2,即t2-3t+2=0(t-1)(t-2)=0
∴t1=1,t2=2(4分)
∴当t=1或t=2时,△PBQ的面积等于2个平方单位.
(2)∵∠ACB=∠PBQ=90°
①若△PBQ∽△ACB
则
| BP |
| CA |
| BQ |
| CB |
| 3-t |
| 3 |
| 2t |
| 6 |
∴t=
| 3 |
| 2 |
此时P点坐标为P(
| 3 |
| 2 |
②若△PBQ∽△BCA
则
| BP |
| CB |
| BQ |
| CA |
| 3-t |
| 6 |
| 2t |
| 3 |
∴t=
| 3 |
| 5 |
此时P点坐标为P(
| 3 |
| 5 |
| 6 |
| 5 |
∴若P、B、Q三点构成的三角形与A、B、C三点构成的三角形相似,此时P和Q
点的坐标分别为P(
| 3 |
| 2 |
| 3 |
| 5 |
| 6 |
| 5 |
点评:本题主要考查了三角形的面积公式,相似三角形的性质,要注意的是(2)中,要根据P点和Q点的不同位置进行分类求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
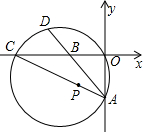 AB的延长线交于点D,弧CD=弧AO,如果AB=10,AO>BO,且AO、BO是x的二次方程x2+kx+48=0的两个根.
AB的延长线交于点D,弧CD=弧AO,如果AB=10,AO>BO,且AO、BO是x的二次方程x2+kx+48=0的两个根.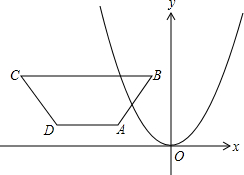
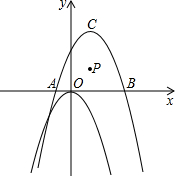 (2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2.
(2007•西城区二模)如图,在直角坐标系内有点P(1,1)、点C(1,3)和二次函数y=-x2. 如图,在直角坐标系内,O为坐标原点,点A的坐标为(1,0),点B在x轴上且在点A的右端,OA=AB,分别过点A、B作x轴的垂线,与二次函数y=x2的图象交于C、D两点,分别过点C、D作y轴的垂线,交y轴于点E、F,直线CD交y轴于点H.
如图,在直角坐标系内,O为坐标原点,点A的坐标为(1,0),点B在x轴上且在点A的右端,OA=AB,分别过点A、B作x轴的垂线,与二次函数y=x2的图象交于C、D两点,分别过点C、D作y轴的垂线,交y轴于点E、F,直线CD交y轴于点H.