题目内容
如图，AB和CD是同一地面上的两座相距39米的楼房，在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°，楼底D的俯角为30°．求楼CD的高（结果保留根号）．分析：在题中两个直角三角形中，知道已知角和其邻边，只需根据正切值求出对边后相加即可．
解答：
解：延长过点A的水平线交CD于点E，则有AE⊥CD，四边形ABDE是矩形，AE=BD=39米．
∵∠CAE=45°，
∴△AEC是等腰直角三角形，
∴CE=AE=39米．
在Rt△AED中，tan∠EAD=
，
∴ED=39×tan30°=13
米，
∴CD=CE+ED=（39+13
）米．
答：楼CD的高是（39+13
）米．
解：延长过点A的水平线交CD于点E，则有AE⊥CD，四边形ABDE是矩形，AE=BD=39米．∵∠CAE=45°，
∴△AEC是等腰直角三角形，
∴CE=AE=39米．
在Rt△AED中，tan∠EAD=
| ED |
| AE |
∴ED=39×tan30°=13
| 3 |
∴CD=CE+ED=（39+13
| 3 |
答：楼CD的高是（39+13
| 3 |
点评：本题考查的是解直角三角形的应用-仰角俯角问题，涉及到特殊角的三角函数值及等腰三角形的判定，熟知以上知识是解答此题的关键．
练习册系列答案
相关题目
11、如图，直线AB和CD被直线MN所截，交点为E和F．则
18、如图所示，一条街道的两个拐角∠ABC和∠BCD，若∠ABC=140°，要使街道AB和CD在同一方向上，需要使∠BCD=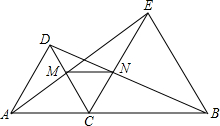
如图，已知C是线段AB上任意一点（C点不与A、B重合），分别以AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE，AE与CD相交于点M，BD与CE相交于点N．求证：
如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．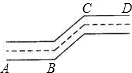
如图所示，一条街道的两个拐角∠ABC和∠BCD，若∠ABC=140°，要使街道AB和CD在同一方向上，需要使∠BCD=________度，根据是________．