题目内容
已知,直线y=-
| ||
| 3 |
 Rt△ABC,∠BAC=90度.且点P(1,a)为坐标系中的一个动点.
Rt△ABC,∠BAC=90度.且点P(1,a)为坐标系中的一个动点.(1)求三角形ABC的面积S△ABC;
(2)证明不论a取任何实数,三角形BOP的面积是一个常数;
(3)要使得△ABC和△ABP的面积相等,求实数a的值.
分析:(1)根据直线的解析式容易求出A,B的坐标,也可以求出OA,OB,AB的长,由于三角形ABC是等腰直角三角形,知道AB就可以求出S△ABC;
(2)不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离1为高,所以三角形BOP的面积是一个常数;
(3)△ABC的面积已知,把△ABP的面积用a表示,就可以得到关于a的方程,解方程可以求出a.
(2)不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离1为高,所以三角形BOP的面积是一个常数;
(3)△ABC的面积已知,把△ABP的面积用a表示,就可以得到关于a的方程,解方程可以求出a.
解答:解:(1)令y=-
x+1中x=0,得点B坐标为(0,1);
令y=0,得点A坐标为(
,0),
由勾股定理得|AB|=2,
∴S△ABC=2;
(2)不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离1为高,
∴S△BOP=
为常数;
(3)当点P在第四象限时,a<0,
∵S△ABO=
,S△APO=-
a,
∴S△ABP=S△ABO+S△APO-S△BOP=S△ABC=2,
即
-
a-
=2,
解得a=
,
当点P在第一象限时,同理可得a=1+
,
综上所述,a的值为
或1+
.
| ||
| 3 |
令y=0,得点A坐标为(
| 3 |
由勾股定理得|AB|=2,
∴S△ABC=2;
(2)不论a取任何实数,△BOP都可以以BO=1为底,点P到y轴的距离1为高,
∴S△BOP=
| 1 |
| 2 |
(3)当点P在第四象限时,a<0,
∵S△ABO=
| ||
| 2 |
| ||
| 2 |
∴S△ABP=S△ABO+S△APO-S△BOP=S△ABC=2,
即
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解得a=
3-5
| ||
| 3 |
当点P在第一象限时,同理可得a=1+
| 3 |
综上所述,a的值为
3-5
| ||
| 3 |
| 3 |
点评:此题主要考查一次函数图象的性质来探讨变化三角形的面积,也结合了方程的知识,解方程就可以求出a.

练习册系列答案
相关题目
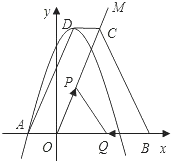 如图,已知抛物线y=a(x-1)2+3
如图,已知抛物线y=a(x-1)2+3
 已知在矩形ABCD中,AB=3,BC=4,以点A为圆心,r为半径作⊙A,
已知在矩形ABCD中,AB=3,BC=4,以点A为圆心,r为半径作⊙A, 根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.
根据要求完成下面的填空:如图,直线AB,CD被EF所截,若已知∠1=∠2.