题目内容
如图,BC是半圆O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E,CE= ,CD=2.
,CD=2.

(1)求直径BC的长;
(2)求弦AB的长.
【答案】
(1) ;(2)
;(2)  .
.
【解析】
试题分析:(1)由勾股定理求得DE的长,根据相似三角形的判定和性质列式求得BC的长;
(2)由△ABE∽△DCE列式求得 ,从而根据勾股定理列方程求解即可.
,从而根据勾股定理列方程求解即可.
试题解析:(1)∵BC是半圆O的直径,∴∠BDC=900.
∵CE= ,CD=2,∴根据勾股定理,得DE=1.
,CD=2,∴根据勾股定理,得DE=1.
∵D是弧AC的中点,∴AD=CD=2.
易证△ADE∽△BCE,∴ ,即
,即 ,解得
,解得 .
.
(2) 易证△ABE∽△DCE, ∴ .
.
设 ,则AB=
,则AB= ,AC=
,AC= ,
,
∵ ,∴
,∴ ,解得
,解得 .
.
∵ ,∴
,∴ .∴AB=
.∴AB= .
.
考点:1.圆周角定理;2. 勾股定理;3.相似三角形的判定和性质.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
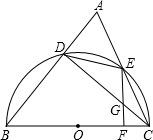 已知:如图,BC是半圆O的直径,D、E是半圆O上两点,
已知:如图,BC是半圆O的直径,D、E是半圆O上两点,
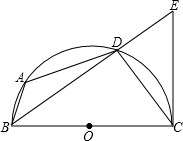 ∠DCE=
∠DCE=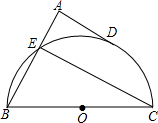 如图,BC是半圆O的直径,点D是半圆上一点,过点D作⊙O切线AD,BA⊥DA于点A,BA交半圆于点E.已知BC=10,AD=4.那么直线CE与以点O为圆心,
如图,BC是半圆O的直径,点D是半圆上一点,过点D作⊙O切线AD,BA⊥DA于点A,BA交半圆于点E.已知BC=10,AD=4.那么直线CE与以点O为圆心,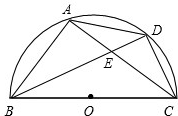 如图,BC是半圆⊙O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E.
如图,BC是半圆⊙O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E. 如图,BC是半圆O的直径,P是BC延长线上一点,PA切⊙O于点A,∠B=30°.
如图,BC是半圆O的直径,P是BC延长线上一点,PA切⊙O于点A,∠B=30°.