题目内容
如图，BC是半圆O的直径，割线EDB交半圆O于D，A是半圆O上一点，AD=DC，EC=3，BD=2.5，tan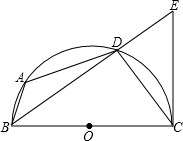
∠DCE=| 2 |
| 5 |
| 5 |
（1）求证：EC是⊙O的切线；
（2）求AB的长．
分析：（1）欲证EC为切线，即证∠ECB=90°．
（2）连接AC交BD与F，根据相似三角形的判定可得到△ADF∽△BCF根据相似比即可求得AB的长．
（2）连接AC交BD与F，根据相似三角形的判定可得到△ADF∽△BCF根据相似比即可求得AB的长．
解答：（1）证明：∵BC为直径
∴∠BDC=∠CDE=90°
∵tan∠DCE=
=
设ED=2
x，DC=5x
∵EC=3
∴ED2+DC2=EC2∴（2
x）2+（5x）2=9
∴x=
∴DE=2，DC=
∵tan∠DBC=
=
=tan∠DCE
∴∠DBC=∠DCE
∴∠DCE+∠DCB=∠DBC+∠DCB=90°
∴EC为切线．
（2）解：连AC交BD于F
由（1）得，AD=DC=
，BC=
∵△ADF∽△BCF
∴
=
=
设DF=2x，则CF=3x
∵CF2-DF2=CD2
∴9x-4x=5
∴x=1
∴DF=2，CF=3
∴BF=
∵AF=
=
∴AB=
=
．
∴∠BDC=∠CDE=90°
∵tan∠DCE=
| ED |
| DC |
2
| ||
| 5 |
设ED=2
| 5 |
∵EC=3
∴ED2+DC2=EC2∴（2
| 5 |
∴x=
| ||
| 5 |
| 5 |
∵tan∠DBC=
| DC |
| BD |
2
| ||
| 5 |
∴∠DBC=∠DCE
∴∠DCE+∠DCB=∠DBC+∠DCB=90°
∴EC为切线．
（2）解：连AC交BD于F
由（1）得，AD=DC=
| 5 |
| 3 |
| 2 |
| 5 |
∵△ADF∽△BCF
∴
| DF |
| CF |
| AD |
| BC |
| 2 |
| 3 |
设DF=2x，则CF=3x
∵CF2-DF2=CD2
∴9x-4x=5
∴x=1
∴DF=2，CF=3
∴BF=
| 1 |
| 2 |
∵AF=
| DF•BF |
| CF |
| 1 |
| 3 |
∴AB=
| BF2-AF2 |
| 1 |
| 6 |
| 5 |
点评：此题主要考查了三角函数、相似的判定、勾股定理以及相交弦定理等知识点的综合运用．
练习册系列答案
名校课堂系列答案
相关题目
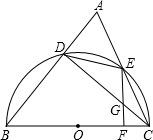已知：如图，BC是半圆O的直径，D、E是半圆O上两点，
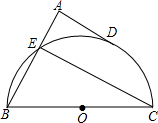如图，BC是半圆O的直径，点D是半圆上一点，过点D作⊙O切线AD，BA⊥DA于点A，BA交半圆于点E．已知BC=10，AD=4．那么直线CE与以点O为圆心，
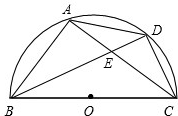如图，BC是半圆⊙O的直径，D是弧AC的中点，四边形ABCD的对角线AC、BD交于点E．
如图，BC是半圆O的直径，P是BC延长线上一点，PA切⊙O于点A，∠B=30°．