题目内容
如图,点E、F分别是矩形ABCD的边AB、BC的中点,连AF、CE交于点G,则 = .
= .
【答案】分析:首先设△AGE为S1,△EGB为S2,△GBF为S3,△CGF为S4,△AGC为S5,依题意可得S1+S2+S3=S2+S3+S4,得出S1=S4.又因为△ABF=△AFC= S矩形ABCD,得出S1+S2+S3=S4+S5.同理可得S2+S3+S4=S4+S5得出S1=S2,S3=S4.故可得S1+S2+S3+S4+2S5=
S矩形ABCD,得出S1+S2+S3=S4+S5.同理可得S2+S3+S4=S4+S5得出S1=S2,S3=S4.故可得S1+S2+S3+S4+2S5= S矩形ABCD,S1+S2+S3+S4=
S矩形ABCD,S1+S2+S3+S4=
 .最后可求得S四边形AGCD:S矩形ABCD的比例.
.最后可求得S四边形AGCD:S矩形ABCD的比例.
解答: 解:连接BG,设△AGE为S1,△EGB为S2,△GBF为S3,△CGF为S4,△AGC为S5.
解:连接BG,设△AGE为S1,△EGB为S2,△GBF为S3,△CGF为S4,△AGC为S5.
∵△ABF= S矩形ABCD=△EBC,∴S1+S2+S3=S2+S3+S4,即S1=S4.
S矩形ABCD=△EBC,∴S1+S2+S3=S2+S3+S4,即S1=S4.
又∵△ABF=△AFC= S矩形ABCD,∴S1+S2+S3=S4+S5
S矩形ABCD,∴S1+S2+S3=S4+S5
同理,S2+S3+S4=S4+S5,而S1=S2,S3=S4.(等底同高)
∴S1+S2+S3+S4+2S5= S矩形ABCD.
S矩形ABCD.
∴S1+S2+S3+S4=
 =
= S矩形ABCD
S矩形ABCD
∴S四边形AGCD:S矩形ABCD=(3-1):3=2:3.
另解:连接BG,设△AGE为S1,△EGB为S2,△GBF为S3,△CGF为S4,△AGC为S5.
∵△ABF=△EBC,∴S1+S2+S3=S2+S3+S4,即S1=S4.
而S1=S2,S3=S4.(等底同高)所以S1=S2=S3=S4
又∵△ABF=△AFC= S矩形ABCD,
S矩形ABCD,
∴S1=S2=S3=S4= S矩形ABCD,
S矩形ABCD,
∴S1+S2+S3+S4= S矩形ABCD,
S矩形ABCD,
S四边形AGCD= S矩形ABCD,
S矩形ABCD,
故答案为: .
.
点评:本题的关键是利用等底同高的三角形的面积相等来求得S1=S2,S3=S4,从而求得S四边形AGCD:S矩形ABCD等于(3-1):3=2:3.
 S矩形ABCD,得出S1+S2+S3=S4+S5.同理可得S2+S3+S4=S4+S5得出S1=S2,S3=S4.故可得S1+S2+S3+S4+2S5=
S矩形ABCD,得出S1+S2+S3=S4+S5.同理可得S2+S3+S4=S4+S5得出S1=S2,S3=S4.故可得S1+S2+S3+S4+2S5= S矩形ABCD,S1+S2+S3+S4=
S矩形ABCD,S1+S2+S3+S4=
 .最后可求得S四边形AGCD:S矩形ABCD的比例.
.最后可求得S四边形AGCD:S矩形ABCD的比例.解答:
 解:连接BG,设△AGE为S1,△EGB为S2,△GBF为S3,△CGF为S4,△AGC为S5.
解:连接BG,设△AGE为S1,△EGB为S2,△GBF为S3,△CGF为S4,△AGC为S5.∵△ABF=
 S矩形ABCD=△EBC,∴S1+S2+S3=S2+S3+S4,即S1=S4.
S矩形ABCD=△EBC,∴S1+S2+S3=S2+S3+S4,即S1=S4.又∵△ABF=△AFC=
 S矩形ABCD,∴S1+S2+S3=S4+S5
S矩形ABCD,∴S1+S2+S3=S4+S5同理,S2+S3+S4=S4+S5,而S1=S2,S3=S4.(等底同高)
∴S1+S2+S3+S4+2S5=
 S矩形ABCD.
S矩形ABCD.∴S1+S2+S3+S4=

 =
= S矩形ABCD
S矩形ABCD∴S四边形AGCD:S矩形ABCD=(3-1):3=2:3.
另解:连接BG,设△AGE为S1,△EGB为S2,△GBF为S3,△CGF为S4,△AGC为S5.
∵△ABF=△EBC,∴S1+S2+S3=S2+S3+S4,即S1=S4.
而S1=S2,S3=S4.(等底同高)所以S1=S2=S3=S4
又∵△ABF=△AFC=
 S矩形ABCD,
S矩形ABCD,∴S1=S2=S3=S4=
 S矩形ABCD,
S矩形ABCD,∴S1+S2+S3+S4=
 S矩形ABCD,
S矩形ABCD,S四边形AGCD=
 S矩形ABCD,
S矩形ABCD,故答案为:
 .
.点评:本题的关键是利用等底同高的三角形的面积相等来求得S1=S2,S3=S4,从而求得S四边形AGCD:S矩形ABCD等于(3-1):3=2:3.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
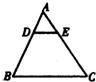 17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=
17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=
 (2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
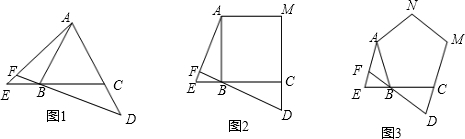
(2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( ) 如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是
如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是